基本介紹
定義,例子,逆矩陣,MATLAB代碼,面積元證明,
定義
在向量分析中,雅可比矩陣是函式的一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。
在代數幾何中,代數曲線的雅可比行列式表示雅可比簇:伴隨該曲線的一個代數群,曲線可以嵌入其中。
它們全部都以數學家卡爾·雅可比命名;英文雅可比行列式"Jacobian"可以發音為[ja ˈko bi ən]或者[ʤə ˈko bi ən]。
假設某函式從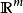 映到
映到 , 其雅可比矩陣是從
, 其雅可比矩陣是從 到
到 的線性映射,其重要意義在於它表現了一個多變數向量函式的最佳線性逼近。因此,雅可比矩陣類似於單變數函式的導數。
的線性映射,其重要意義在於它表現了一個多變數向量函式的最佳線性逼近。因此,雅可比矩陣類似於單變數函式的導數。
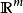



假設 是一個從n維歐氏空間映射到到m維歐氏空間的函式。這個函式由m個實函式組成:
是一個從n維歐氏空間映射到到m維歐氏空間的函式。這個函式由m個實函式組成: 。這些函式的偏導數(如果存在)可以組成一個m行n列的矩陣,這個矩陣就是所謂的雅可比矩陣:
。這些函式的偏導數(如果存在)可以組成一個m行n列的矩陣,這個矩陣就是所謂的雅可比矩陣:



此矩陣用符號表示為:
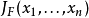
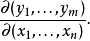


例子
由球坐標系到直角坐標系的轉化由F函式給出︰




此坐標變換的雅可比矩陣是

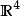


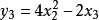

其雅可比矩陣為:

此例子說明雅可比矩陣不一定為方陣。
逆矩陣
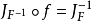
成立。相反,倘若雅可比行列式在某一個點不為零,那么該函式在這個點的某一鄰域內可逆(存在反函式)。
一個多項式函式的可逆性與非經證明的雅可比猜想有關。其斷言,如果函式的雅可比行列式為一個非零實數(相當於其不存在復零點),則該函式可逆且其反函式也為一個多項式。
MATLAB代碼
MATLAB中jacobian是用來計算Jacobi矩陣的函式。
syms r l f
x=r*cos(l)*cos(f);
y=r*cos(l)*sin(f);
z=r*sin(l);
J=jacobian([x;y;z],[r l f])
結果:
J =
[ cos(l)*cos(f), -r*sin(l)*cos(f), -r*cos(l)*sin(f)]
[ cos(l)*sin(f), -r*sin(l)*sin(f), r*cos(l)*cos(f)]
[ sin(l), r*cos(l), 0 ]
面積元證明
二維下dx(u,v)dy(u,v)=Jdudv成立
證明:對於曲面x=x(u,v),y=y(u,v),取它的微元,即小曲邊四邊形ABCD,其中
A(u,v),B(u+△u,v),C(u+△u,v+△v),D(u,v+△v),這個曲邊四邊形ABCD可以近似看成由微小向量B(u+△u,v)-A(u,v)和D(u,v+△v)-A(u,v)張成。
利用中值定理可知:
(u+△u,v)-(u,v)=Mdu
(u,v+△v)-(u,v)=Ndv
式中M,N為偏導數形式,可以通過簡單計算得出。
當變化量很小時,
將(u+△u,v)-(u,v)近似看為dx(u,v)
(u,v+△v)-(u,v)近似看為dy(u,v),
故dx(u,v)dy(u,v)=M*Ndudv
式中M*N為二維Jacobi行列式的展開形式。
由此得證。