階梯型矩陣是矩陣的一種類型。他的基本特徵是如果所給矩陣為階梯型矩陣則矩陣中每一行的第一個不為零的元素的左邊及其所在列以下全為零。
基本介紹
- 中文名:階梯型矩陣
- 外文名:Row-Echelon Matrix
- 類型:模型
- 條件:需滿足兩個條件
- 用途:計算
簡介
畫法
 畫法1
畫法1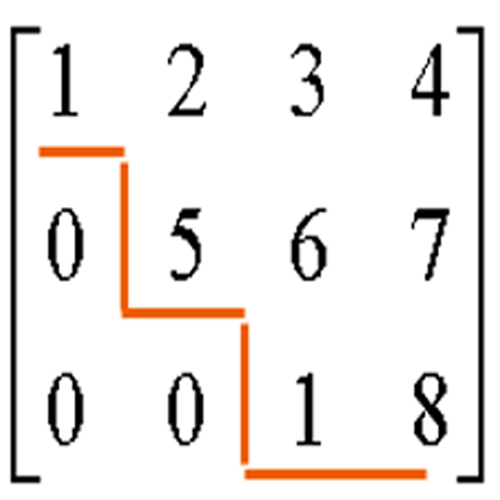 畫法2
畫法2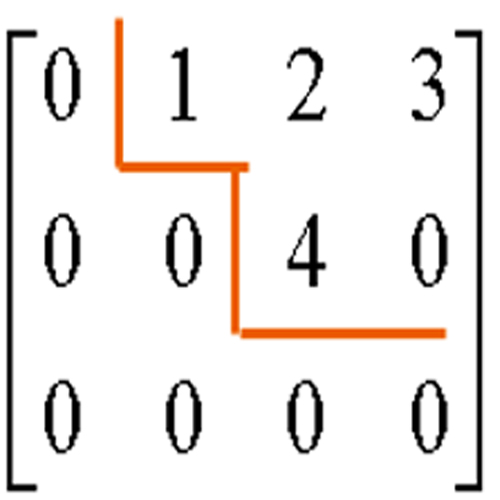 畫法3
畫法3階梯型矩陣是矩陣的一種類型。他的基本特徵是如果所給矩陣為階梯型矩陣則矩陣中每一行的第一個不為零的元素的左邊及其所在列以下全為零。
 畫法1
畫法1 畫法2
畫法2 畫法3
畫法3若矩陣A滿足兩條件:(1)它是階梯形矩陣;(2)非零首元所在的列除了非零首元外,其餘元素全為0,則稱此矩陣A為行簡化階梯形矩陣。...
階梯型矩陣是矩陣的一種類型。他的基本特徵是如果所給矩陣為階梯型矩陣則矩陣中每一行的第一個不為零的元素的左邊及其所在列以下全為零。...
最簡行階梯矩陣,是一種特殊的行階梯矩陣,其各行的第1個非零元素均為1,且所在列的其他元素都為0。...
若有一個矩陣滿足(1)是階梯形矩陣;(2)所有的非零行的第一個非零元素均為1,且其所在列中的其他元素都是零。 任何一個非零矩陣總可以經過有限次初等變換為...
在階梯形矩陣中,若非零行的第一個非零元素全是1,且非零行的第一個元素1所在列的其餘元素全為零,就稱該矩陣為行最簡形矩陣。 例如矩陣:...
行階梯形形式(row echelon form)行階梯形形式需要滿足以下兩個條件:1)元素全為零的行在矩陣的底部2)如果相鄰兩行為非零行,則靠下的行的左邊以更多的零元素開始...
定義1. 在m*n矩陣A中,任意決定α行和β列交叉點上的元素構成A的一個k階子矩陣,此子矩陣的行列式,稱為A的一個k階子式。例如,在階梯形矩陣中,選定1,3行...
高斯消元法也是一種矩陣分解方法。通過初等變換操作,可以將任何矩陣變為階梯形矩陣,而每個操作可以看做是將矩陣乘上一個特定的初等矩陣。奇異值分解則是另一種分解...
行階梯形矩陣,Row-Echelon Form,是指線性代數中的某一類特定形式的矩陣。...... 在階梯形矩陣中,若非零行的第一個非零元素全是1,且非零行的第一個元素1所在...
1.1.2矩陣與向量31.1.3矩陣的基本運算.41.2矩陣的初等變換.61.2.1初等行變換與階梯型矩陣.71.2.2初等行變換的兩個套用9...
將階梯式策略引入到多模型廣義預測控制器中,不僅不需要矩陣求逆,大大減小了計算...狀態空間描述比較有利於系統的穩定性分析,在噪聲強度不大和無結構型建模誤差的...
對齊次線性方程組的係數矩陣施行初等行變換化為階梯型矩陣後,不全為零的行數r(即矩陣的秩)小於等於m(矩陣的行數),若m<n,則一定n>r,則其對應的階梯型n-r...
Gallager曾給出了一個碼長為20的規則(3,4)LDPC碼的校驗矩陣,如圖所示。圖中的第一個子矩陣就是一個階梯型矩陣,而第2個和第3個矩陣都是第一個子矩陣的列...
二次型用標準型表示。矩陣向階梯型,對角形,單位矩陣方向化簡。4數據元降維計算(6)主要是用排列組合與遞推或歸納法對多維數據元降維計算。...
《線性代數題型全攻略》與同濟版《線性代數》同步,包括行列式、矩陣及其運算、矩陣的初等變換與線性方程組、向量組的線性相關性、相似矩陣及二次型、線性空間與線性...
一般來說,一個矩陣經過初等行變換後就變成了另一個矩陣,當矩陣A經過初等行變換變成矩陣B時,一般寫作可以證明:任意一個矩陣經過一系列初等行變換總能變成階梯型矩陣...
埃爾米特形式(Hermite Normal form)複流形上的一種特殊雙線性形式。...線上性代數中,埃爾米特形式是整數Z上矩陣的簡化階梯形式的一個類似形式。就像...
c.伴隨矩陣集合={轉置矩陣,逆矩陣,伴隨矩陣;簡化階梯形,相似對角陣或 者契約對角陣} ③常量矩陣 a.0矩陣(加法0元):元素全是零的矩陣稱為零距陣.可記作...
第1章 線性方程組與矩陣 1.1 概述 1.2 二元和三元線性方程組解的幾何意義 1.3 高斯消元法與階梯形方程組 1.4 矩陣及矩陣的初等變換 1.4.1 矩陣的概念及...
