行階梯形矩陣,Row-Echelon Form,是指線性代數中的某一類特定形式的矩陣。
基本介紹
- 中文名:行階梯形矩陣
- 外文名:Row-Echelon Form
- 學科:線性代數
- 簡稱:階梯形矩陣
階梯形矩陣
定義
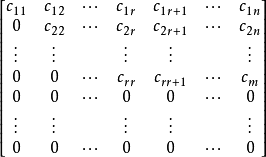
舉例
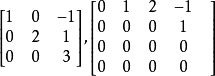
區分
行最簡形矩陣

標準形矩陣

行階梯形矩陣,Row-Echelon Form,是指線性代數中的某一類特定形式的矩陣。
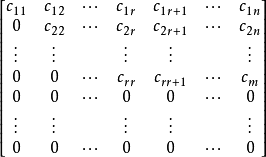
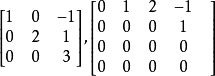


行階梯形矩陣,Row-Echelon Form,是指線性代數中的某一類特定形式的矩陣。...... 在階梯形矩陣中,若非零行的第一個非零元素全是1,且非零行的第一個元素1所在...
最簡行階梯矩陣,是一種特殊的行階梯矩陣,其各行的第1個非零元素均為1,且所在列的其他元素都為0。...
階梯型矩陣是矩陣的一種類型。它的基本特徵是如果所給矩陣為階梯型矩陣則矩陣中每一行的第一個不為零的元素的左邊及其所在列以下全為零。...
行最簡形矩陣,Line minimalist matrix,是指線性代數中的某一類特定形式的矩陣。...... 在階梯形矩陣中,若非零行的第一個非零元素全是1,且非零行的第一個元素...
行階梯形形式(row echelon form),摘自Elementary Linear Algebra》。...... 行階梯形形式需要滿足以下兩個條件:1)元素全為零的行在矩陣的底部2)如果相鄰兩行為非...
若有一個矩陣滿足(1)是階梯形矩陣;(2)所有的非零行的第一個非零元素均為1,且其所在列中的其他元素都是零。 任何一個非零矩陣總可以經過有限次初等變換為...
定義1:用初等行變換將矩陣A化為階梯形矩陣, 則矩陣中非零行的個數就定義為這個矩陣的秩, 記為r(A),根據這個定義, 矩陣的秩可以通過初等行變換求得。需要注意...
定義1. 在m*n矩陣A中,任意決定α行和β列交叉點上的元素構成A的一個k階子矩陣,此子矩陣的行列式,稱為A的一個k階子式。例如,在階梯形矩陣中,選定1,3行...
若矩陣A滿足兩條件:(1)它是階梯形矩陣;(2)非零首元所在的列除了非零首元外,其餘元素全為0,則稱此矩陣A為行簡化階梯形矩陣。...
高斯消元法也是一種矩陣分解方法。通過初等變換操作,可以將任何矩陣變為階梯形矩陣,而每個操作可以看做是將矩陣乘上一個特定的初等矩陣。奇異值分解則是另一種分解...
對齊次線性方程組的係數矩陣施行初等行變換化為階梯型矩陣後,不全為零的行數r(即矩陣的秩)小於等於m(矩陣的行數),若m<n,則一定n>r,則其對應的階梯型n-r...
計算矩陣A的秩的最容易的方式是高斯消去法,即利用矩陣的初等變換生成一個行階梯形矩陣,由於矩陣的初等變換不改變矩陣的秩,因此A的行梯陣形式有同A一樣的秩。...
通過計算,可以將增廣矩陣轉換為簡化行階梯形式,即把左邊轉化為單位矩陣:求得B為A的逆矩陣。高斯消元法其他套用 編輯 高斯消元法找出逆矩陣 高斯消元法可以用來...
一般來說,一個矩陣經過初等行變換後就變成了另一個矩陣,當矩陣A經過初等行變換變成矩陣B時,一般寫作可以證明:任意一個矩陣經過一系列初等行變換總能變成階梯型矩陣...
定義 A的行空間的維數稱為矩陣A的秩(rank)。為求矩陣的秩,可以將矩陣化為行階梯形矩陣,行階梯形矩陣中的非零行將構成行空間的一組基。...
②矩陣消元法.將線性方程組的增廣矩陣通過行的初等變換化為行簡化階梯形矩陣 ,則以行簡化階梯形矩陣為增廣矩陣的線性方程組與原方程組同解。當方程組有解時,將...
埃爾米特形式(Hermite Normal form)複流形上的一種特殊雙線性形式。...線上性代數中,埃爾米特形式是整數Z上矩陣的簡化階梯形式的一個類似形式。就像...
第三章 矩陣的初等變換與線性方程組 一、知識要點 二、方法歸納 三、題型攻略 (題型1化矩陣為行階梯形或行最簡形) (題型2涉及初等矩陣或初等變換的題型...
