基本介紹
- 中文名:阿貝爾判別法
- 外文名:Abel Discriminance
- 提出者:尼爾斯·亨利克·阿貝爾
- 套用學科:微積分
- 適用領域範圍:級數,積分
在級數中的套用
數項級數收斂性的阿貝爾判別法
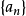


函式項級數收斂性的阿貝爾判別法





在積分中的套用
反常積分收斂性的阿貝爾判別法


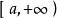

反常含參積分一致收斂性的阿貝爾判別法




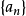









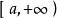





阿貝爾判別法(Abel Discriminance)是分析學中一條十分重要的判定法則,與狄利克雷判別法(Dirichlet Discriminance)合稱為A-D判別法。主要用於判定數項級數的收斂、...
阿貝爾變換是一個恆等式,它在數學分析中有著廣泛的套用。通過阿貝爾變換,可以分別證明任意項級數收斂的阿貝爾判別法和狄利克雷判別法。...
阿貝爾變換是一個恆等式,它在數學分析中有著廣泛的套用。通過阿貝爾變換,可以分別證明任意項級數收斂的阿貝爾判別法和狄利克雷判別法阿貝爾變換也叫分部求和法(Abel ...
一致收斂判別法是判定函式列與函式項級數是否收斂的重要方法,其中比較著名的有柯西準則、魏爾斯特拉斯判別法以及阿貝爾判別法等,它們是數學分析中重要的理論基礎。...
根值判別法,又稱柯西判別法,是判斷正項級數收斂性的一種重要方法。正項級數收斂性判別法主要有根式判別法、比式判別法、阿貝爾判別法、積分判別法和對數判別法等...
杜·布瓦-雷蒙判別法是級數收斂的判別法之一。此判別法由杜·布瓦-雷蒙(Du Bois-Reymond,P.D.G.)建立。...
是否收斂。下面將介紹5種判別級數是否收斂的方法。[1] (1)【阿貝爾判別法】若 為單調有界數列,且級數 收斂,則級數 收斂。(2)【狄利克雷判別法】若...
2 絕對收斂級數及其性質 ▪ 定理2 ▪ 例1 3 阿貝爾判別法和狄利克雷判別法 ▪ 定理3(阿貝爾判別法) ▪ 定理4(狄利克雷判別法) 一般...
一致收斂性是函式列或函式項級數的一種性質。一致收斂函式的判別方法有很多種,最常見的有Cauchy判別法、Abel判別法、Dirichlete判別法等。一致收斂函式具有連續性、...
一.無界函式廣義積分的概念,柯西判別法 二.阿貝爾判別法和狄立克萊判別法 習題 第二部分函式項級數 第十一章 函式項級數.冪級數 §1.函式項級數的一致收斂 一....
這個級數收斂於一個開放的單位圓盤|z|<1 以及圓 |z|=1 ,z=-1除外 (根據阿貝爾判別法),而且這裡的收斂對每個半徑小於一的圓盤是一致的。...
3.反常積分的絕對收斂和條件收斂.阿貝爾判別法和狄利克雷判別法第十一講4.第二類反常積分5.反常積分的變數變換及分部積分第十章 曲線的長度第十二講...
有關一致收斂的判別法及性質,以函式列情形為主簡介如下,其他情形是類似的。常用判別一致收斂的準則及判別法有:柯西準則,M判別法,狄利克雷判別法,阿貝爾判別法與...
除了柯西準則和餘項準則外,還可以通過Weierstrass判別法、Abel判別法和Dirichlet判別法來判別函式項級數是否一致收斂。中文名 一致收斂 外文名 Uniform Convergence ...
無窮積分的性質與收斂判別 一 無窮積分的性質 二 比較判別法 三 狄利克雷判別法與阿貝爾判別法 3 瑕積分的性質與收斂判別附錄Ⅰ 微積分學簡史附錄Ⅱ 實數理論 ...
2.2 Abel方法在級數收斂性判別中的套用 2.2.1 數項級數收斂性的判別法. 2.2.2 函式項級數一致收斂性判別法 習題2.2. 2.3 Abel方法在廣義積分收斂...
第3節 廣義積分收斂性的狄利克雷判別法和阿貝爾判別法的套用第4節 絕對收斂性和條件收斂性的判別第5節 廣義積分收斂性質的理論方法自我鞏固拓?提高練習...
狄利克雷判別法和阿貝爾判別法 §9.4 數項級數的性質 9.4.1 結合律 9.4.2 交換律 9.4.3 級數的乘法(分配律) §9.5 無窮乘積 習題九第十章 函式...
