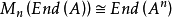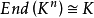在抽象代數中，由End（X）表示的阿貝爾群體X的自同態環（endomorphism ring）是X所有同態的集合，賦予由點加法定義的加法運算的函式和由函式組合定義的乘法運算。 通過這些運算，阿貝爾組的自同態環就形成了單位環，零映射作為加性成分，本體映射作為乘法成分。
所涉及的功能僅限於在上下文中定義的同態的定義，這取決於所考慮的對象的類別。 自同態環因此就編碼了對象的幾個內部屬性。 由於所得到的對象通常是某個環R上的代數，所以這也可以稱為內生代數。
基本介紹
- 中文名：自同態環
- 外文名：endomorphism ring
- 學科：數學
- 實質：所有同態的集合
- 別稱：內生代數
- 相關名詞：阿貝爾
簡介,說明,屬性,舉例,
簡介
在抽象代數中，由End（X）表示的阿貝爾群體X的自同態環是X所有同態的集合，賦予由點加法定義的加法運算的函式和由函式組合定義的乘法運算。 通過這些運算，阿貝爾組的自同態環就形成了單位環，零映射作為加性成分，本體映射作為乘法成分。
所涉及的功能僅限於在上下文中定義的同態的定義，這取決於所考慮的對象的類別。 自同態環因此就編碼了對象的幾個內部屬性。 由於所得到的對象通常是某個環R上的代數，所以這也可以稱為內生代數。
說明
讓（A，+）成為一個阿貝爾組，我們認為從A到A的群體是同態的。然後加上兩個這樣的同態可以被定義為產生另一個群體同態。 顯然，給定兩個這樣的同態f和g，f和g的和是同態（f + g）（x）：= f（x）+ g（x）。 在這個操作結束（A）是一個阿貝爾組。 隨著同態組合的附加操作，End（A）是具有乘法身份的環。 這個組合是明確的（fg）（x）：= f（g（x））。 乘法身份是A上的身份同態。
如果集合A不形成阿貝爾組，則上述構造不一定是加性的，因此兩個同態的總和不一定是同態的。這是一個同態但不是一個環的典型例子。
屬性
（1）自同態環總是具有加性和乘法的身份，分別為零映射和本體映射。
（2）內相環是締合的，但通常是非交換性的。如果一個模組很簡單，那么它的同構環就是一個劃分環（這有時叫做Schur的引理）。若且唯若其同形環不包含任何不平凡的冪等元素時，模組是不可分解的。
（3）對於一個半模組，內同環是馮·諾依曼常規環。
（4）非零模組的自同態環具有一個或兩個最大正確的理想。如果模組是尼恩，諾特，則同態環具有獨特的最大理想，因此它是一個本地環。
（5）尼恩統一模組的同構環是一個本地環。
（6）具有有限組成長度的模組的同形環是半主環。
（7）如果R模組有限生成和投影（即進程發生器），則模組的同態環和R共享所有森田不變屬性。森田理論的一個根本結果是，與R相當的所有環都作為內同環產生。
舉例
在R模組的類別中，R模組M的同構環將僅使用R模組同態，這通常是阿貝爾群同態的子集。 當M是有限生成的投影模組時，內同環是森田對模組類別的核心。
對於任何阿貝爾組A，
，因為
中的任何矩陣都攜帶自然同態結構
如下：
它和下式相等
人們可以使用這個同構構造很多非同態環。
此外，當
是一個欄位時，有一個規範的同構
，所以
， 用n×n矩陣的環來識別K向量空間。更一般地，自由模組
的內同構代數自然是
矩陣。
作為最後一點的一個具體例子，對於具有統一性的任何環R，End（RR）= R，其中R的元素通過左乘法作用在R上。
一般來說，可以為任何預先添加類別的對象定義同形態環。
