羅氏平行直線(Lobachevskian parallel lines)是羅氏幾何的主要研究對象。羅氏平面幾何的平行直線和歐氏平面幾何的平行直線的定義是不相同的，在羅氏平面幾何中，所謂已知直線的平行直線，只是與已知直線不相交的所有直線中的特殊直線。
基本介紹
- 中文名：羅氏平行直線
- 外文名：Lobachevskian parallel lines
- 所屬學科：數學
- 所屬問題：高等幾何(非歐幾里得幾何)
基本概念,羅氏平行直線的基本性質,
基本概念
在羅氏平面上，若
∥
，則稱直線AP沿 方向(或 方向)平行於直線BC，記為AP∥BC於方向 (或 )。當方向一致時，直線間的平行具有對稱性和傳遞性。在羅氏平面上，過直線CC′外一點A，有且僅有兩條直線AP和AQ分別於不同的方向平行於CC′，在羅氏平面上，任何兩對平行線可以互相疊合，且二平行線在平行方向上無限接近，而在反方向無限遠離。
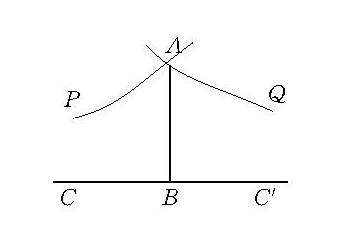圖1羅氏平行直線的基本性質
定理1 (羅氏直線平行關係的對稱性定理) 若P'P //
於方向，則Q'Q//P'P於同方向，即方向。
定理2(羅氏直線平行關係的傳遞性定理) 對於不同的三條直線P'P，Q'Q和R'R，若P'P//Q'Q於方向
，Q'Q//R'R於同方向，則P'P //R'R於同方向。
定理3 任何兩對平行直線可以互相疊合(即它們作為點的集合是契約的圖形)。
定理4設P'P //Q'Q於方向，則在直線P'P上點M到直線Q'Q的距離，當M點沿平行方向移動是遞減，反之遞增。
雖然在中學數學課本中，關於羅氏平行直線的定義一點都沒有談及，但是卻簡單描述了羅氏平行直線的性質：兩條平行線，在一側無限接近，而在另一側無限遠離，非常直觀地描述了兩條平行直線的位置關係，易於學生理解，但羅氏平行直線的基本性質基本沒有提及，更談不上系統性地論述。
