基本介紹
- 中文名:羅氏平行射線
- 外文名:Lobachevskian parallel half line
- 所屬學科:數學
- 所屬問題:高等幾何(非歐幾里得幾何)
- 簡介:指羅氏平面上互相平行的兩條射線
基本概念,羅氏平行射線的基本性質,
基本概念
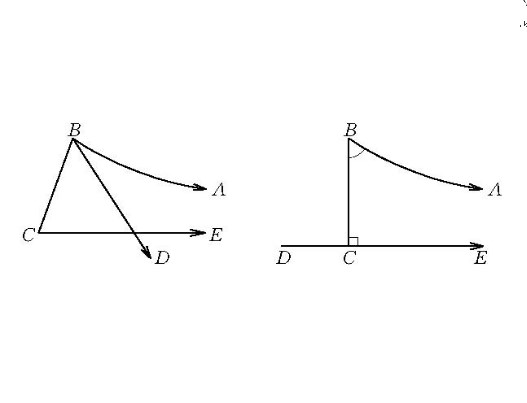
定義1 若共面的兩條射線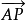 和
和 在直線
在直線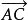 的同側並且不相交,而在∠CAP的內部的任意射線
的同側並且不相交,而在∠CAP的內部的任意射線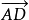 均與
均與 相交,則稱
相交,則稱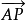 平行於
平行於 ,記作
,記作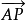 ∥
∥ 。
。
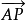

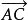
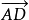

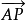

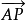

設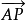 ∥
∥ ,當
,當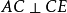 時,則稱∠CAP為線段AC的平行角,而線段AC稱為∠CAP的平行距。
時,則稱∠CAP為線段AC的平行角,而線段AC稱為∠CAP的平行距。
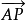

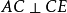
定義3 若射線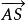 上的點到直線BC的距離無上界,則稱射線
上的點到直線BC的距離無上界,則稱射線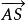 和直線BC是分散的。
和直線BC是分散的。
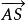
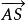
羅氏平行射線的基本性質
由平行射線的定義可知:若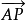 ∥
∥ ,則
,則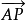 ∥
∥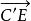 ,其中
,其中 或
或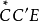 。
。
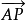

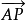
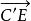

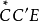
定理1 設點A不在直線CE上,則存在唯一一條射線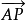 ∥
∥ 。
。
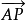

推論:若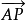 ∥
∥ 並且
並且 ,則
,則 。
。
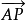



定理2平行角是銳角。
定理3 對於任意直線CE與不在其上的點A,存在無窮多條直線通過A點,並與直線CE共面不相交。
定理4 設 並且AP∥CE,則當
並且AP∥CE,則當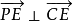 時,AC>PE。
時,AC>PE。

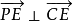
定理5 若直線AS和直線BC相交,則射線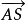 和直線
和直線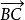 是分散的。
是分散的。
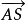
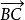
定理6 設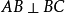 ,P與C兩點在直線AB的同側,則
,P與C兩點在直線AB的同側,則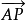 ∥
∥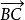 的充分必要條件是AP和直線BC是不分散的。
的充分必要條件是AP和直線BC是不分散的。
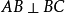
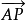
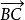
定理7 若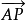 ∥
∥ ,則
,則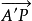 ∥
∥ ,其中
,其中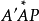 或
或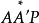 。
。
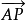

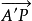

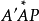
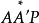
定理8 設一條直線B'B和它的一條斜射線 ,則恰有
,則恰有 的一條分界垂線(
的一條分界垂線(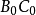 即
即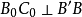 並且MN∥
並且MN∥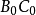 ,於方向
,於方向 。)
。)