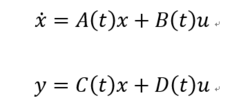簡介
嚴格地說,一切實際的系統都是非線性的,真正的線性系統在現實世界是不存在的。但是,很大一部分實際系統,它們的某些主要關係特性,在一定的範圍內,可以充分精確地用線性系統來加以近似地代表。並且,實際系統與理想化了的線性系統間的差別,對於所研究的問題而言已經小到無關緊要的程度而可予以忽略不計。
因此,從這個意義上說,線性系統或者可線性化的系統又是大量存在的,而這正是研究線性系統的實際背景。
線性變參數控制,又稱為線性時變控制,即同時滿足線性系統和時變系統特徵的控制方法,它滿足控制系統疊加性與均勻性的特點,同時,當某個參數值隨時間而變化時,整個特性也隨時間而變化。
變參數控制可滿足各種負荷或干擾的條件下對控制質量的要求,使控制過程質量最佳,可利用可程式序調節器具有的判斷和運算能力,根據對象的要求,對參數加以適當的改變,從而提高控制質量。
線性時變控制理論
線性時變控制理論是系統與控制理論中最為成熟和最為基礎的一個組成分支,是現代控制理論的基石。
系統與控制理論的其他分支,都不同程度地受到
線性控制理論的概念、方法和結果的影響和推動。
系統是由相互關聯和相互作用的若干組成部分按一定規律組合而成的具有特定功能的整體。系統可具有完全不同的屬性,如工程系統、
生物系統、
經濟系統、社會系統等。但是,在系統理論中,常常抽去具體系統的物理或社會含義而把它抽象化為一個一般意義下的系統而加以研究,這種處理方法有助於揭示系統的一般特性。
系統最基本的特徵是它的整體性,系統的行為和性能是由其整體所決定的,系統可以具有其組成部分所沒有的功能,有著相同組成部分但它們的關聯和作用關係不同的兩個系統可呈現出很不相同的行為和功能。
在系統與控制理論中,我們將主要研究
動態系統,通常也稱其為動力學系統。動態系統常可用一組微分方程或差分方程來表征,並且可對系統的運動和各種性質給出嚴格和定量的數學描述。當描述動態系統的數學方程具有線性屬性時,稱相應的系統為線性系統。線性系統是一類最簡單且研究得最多的動態系統。
控制方法
簡單說,線性變參數控制主要研究線性變參數系統狀態的運動規律和改變這種運動規律的可能性方法,建立和揭示
系統結構、參數、行為和性能間的確定的和定量的關係。在對系統進行研究的過程中,建立合理的
系統數學模型是首要的前提,對於
線性系統,常用的模型有時間域模型和頻率域模型,時間域模型比較直觀,而頻率域模型則是一個更強大的工具,二者建立的基本途徑一般都通過解析法和實驗法。
數學模型提供了解決問題的可能性,在此基礎上,還需要在系統中加入控制部分來達到期望的性能,這些都可以先在數學模型中加入一些環節,再在實際中實現。
經典的
線性控制理論以
拉普拉斯變換為主要工具,在50年代業已成熟。後來,一些新的數學工具相繼得到了運用,先進的計算機技術也被使用起來,這些都推動了線性系統理論的進一步發展和在實際中的廣泛運用。
本世紀50年代,經典的線性系統理論已經發展成熟和完備,並在不少工程技術領域中得到了成果的套用。其數學基礎是拉普拉斯變換,模型是傳遞函式,分析和綜合方法是
頻率回響法。但是,它具有明顯的局限性,突出的是難於解決多輸入—多輸出系統,並且難以揭示系統的更深刻的特性。
在50年代蓬勃興起的航天技術的推動下,線性系統理論在1960前後開始了從經典到現代階段的過渡,其重要標誌之一是
卡爾曼(R.E.Kalman)系統地把
狀態空間法引入到系統和控制理論中來。並在此基礎之上,卡爾曼進一步提出了能控性和能觀測性這兩個表征系統結構特性地重要概念,已經證明這是線性系統理論中的兩個最基本的概念。建立在狀態空間法基礎上的線性系統的分析和綜合方法通常稱為現代線性系統理論。
自60年代中期以來,線性系統理論不僅在研究內容還是在研究方法上,又有了一系列新的發展。出現了這種從幾何方法角度來研究線性系統的結構和特性的幾何理論,出現了以抽象代數為工具的代數理論。也出現了在推廣經典頻率法基礎上發展起來的多變數頻域理論。與此同時,隨著計算機技術的發展和普及,線性系統分析和綜合中的計算問題,以及利用計算機對線性系統進行輔助分析和輔助設計的問題,也都得到了廣泛和充分的研究。
線性時變系統
線性系統是指同時滿足疊加性與均勻性(又稱為其次性)的系統。所謂疊加性是指當幾個輸入信號共同作用於系統時,總的輸出等於每個輸入單獨作用時產生的輸出之和;均勻性是指當輸入信號增大若干倍時,輸出也相應增大同樣的倍數。
時變系統(time-varying system)其中一或一個以上的參數值隨時間而變化,從而整個特性也隨時間而變化的系統。時變系統的特點是,其輸出回響的波形不僅同輸入波形有關,而且也同輸入信號加入的時刻有關。
線性時變系統即同時滿足線性系統和時變系統特徵的系統,它滿足系統疊加性與均勻性的特點,同時,當系統中某個參數值隨時間而變化時,整個特性也隨時間而變化。
狀態方程
n維線性時變系統的狀態方程為:
其中,u是p維輸入向量,y是q維輸出向量。A、B、C、D分別是線性系統的參數,均是時間t的函式,即參數隨時間的變化 變化。
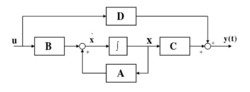
結構圖
線性時變系統的結構圖如下:
控制穩定性
穩定性是設計控制系統的最基本要求。
線性時變系統方程:
如果已經求出矩陣A(t)的所有特徵值,系統漸近穩定的充要條件是:A(t)的所的特徵值都位於S的左半平面。