基本介紹
- 中文名：
- 外文名：
- 提出者：
- 提出時間：
- 適用領域：流體力學
- 簡稱：
N-S方程定義,影響意義,求解方法,基本假設,參考文獻,
N-S方程定義
影響意義
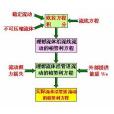
求解方法
對於雷諾數
的情況，方程左端的加速度項與粘性項相比可忽略，從而可求得斯托克斯流動的近似解。RA·密立根【羅伯特·安德魯·密立根】根據這個解給出了一個有名的套用（密立根油滴實驗），即空氣中細小球狀油滴的緩慢流動。
基本假設
在解釋納維-斯托克斯方程的細節之前，首先，必須對流體作幾個假設。第一個是流體是連續的。這強調它不包含形成內部的空隙，例如，溶解的氣體氣泡，而且它不包含霧狀粒子的聚合。另一個必要的假設是所有涉及到的場，全部是可微的，例如壓強
，速度
，密度
，溫度
，等等。該方程從質量，動量守恆，和能量守恆的基本原理導出。對此，有時必須考慮一個有限的任意體積，稱為控制體積，在其上這些原理很容易套用。該有限體積記為
，而其表面記為
。該控制體積可以在空間中固定，也可能隨著流體運動。
