基本介紹
- 中文名:庫埃特流動
- 外文名:Couette flow
- 別名:拖拽流動
- 學科分類:物理學
- 領域:流體動力學
- 套用:物理及工程課程
簡介
平面庫埃特流動

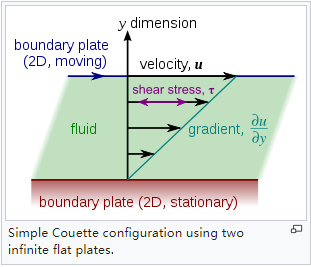

庫埃特流動啟動
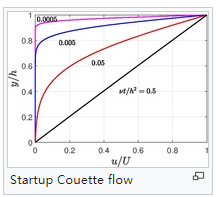





庫埃特流動與壓力梯度



庫埃特流動與矩形通道
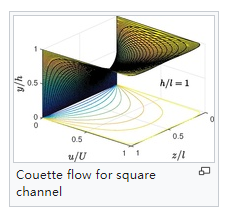



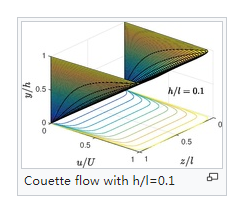



















庫埃特流動是指粘性流體在相對運動著的兩平行平板之間的層流流動。在流體動力學中,庫埃特流動是兩個表面之間的空間中粘性流體的流動,其中一個流體相對於另一個表面正切向移動。庫埃特流動這種流動類型是為了紀念 Maurice Ma...
在流體力學中,泰勒-庫埃特流由夾在兩個旋轉圓柱之間縫隙中的粘性流體組成。當角速度較低時,通過測量雷諾數Re,可知這種流動具有穩定性和方位性。這種基本狀態被稱作環狀庫埃特流,是因為莫里斯・庫埃特曾用這套實驗裝置測量粘度。傑弗...
庫埃特流 庫埃特流(Couette flow)是1993年發布的力學名詞,出自《力學名詞》第一版。公布時間 1993年經全國科學技術名詞審定委員會審定發布。出處 《力學名詞》第一版。
對於可以線性化的情況,如運動的無限平板所造成的粘性流,渦絲在粘性流內的擴散過程,非定常庫埃特流和埃克曼流等,曾得出極少量的解析形式的結果。電子計算機的套用以及理論流體力學和計算流體力學的發展促進了非定常流動的理論研究。線...
對於可以線性化的情況,如運動的無限平板所造成的粘性流,渦絲在粘性流內的擴散過程,非定常庫埃特流和埃克曼流等,曾得出極少量的解析形式的結果。電子計算機的套用以及理論流體力學和計算流體力學的發展促進了非定常流動的理論研究。線...
平行流動的穩定性 平行流動包括圓管內的泊肅葉流動,兩平行平板間的泊肅葉流動、庫埃特流動以及二者的組合。邊界層中的層流嚴格地說不是平行流動,因為它的流線並不嚴格平行,但常用同樣方法處理。這類流動的特點是一旦失穩,立即轉變為...
粘彈性流體的庫埃特流動和泊肅葉流動均屬這種流動。例如在自由面上,粘彈性效應能以外森伯效應的形式表現出來,即粘彈性流體有沿旋轉棒向上爬的傾向。如果把牛頓流體放入容器,它會沿容器壁向上爬升。粘彈性流體從管內自由流出時,通常可以...
2.1.1庫埃特流動 2.1.2泊肅葉流動 2.2運動平板引起的流動 2.2.1突然加速平板引起的流動(斯托克斯第一問題)2.2.2振動平板引起的流動(斯托克斯第二問題)2.3平面駐點流動(希門茨流動)2.4重力作用下的平行流動 2.5平行平面間的...
1.2 流動的基本方程組 1.2.1 質量守恆與動量方程 1.2.2 變形速度張量 1.2.3 牛頓流體本構方程 1.2.4 無量綱方程 1.3 平行流動 1.3.1 泊肅葉流動 1.3.2 庫埃特流動 1.4 黏性不可壓縮流體繞圓球運動...
6.1 黏性流動的相似性和無量綱參數 150 6.2 平行定常流動 151 6.2.1 泊肅葉流動 151 6.2.2 庫埃特流動 153 6.2.3 庫埃特-泊肅葉流動 154 6.3 平行非定常流動 156 6.3.1 突然加速平板引起的流動(斯托克斯**問題)...
的流動44 132納維斯托克斯方程中的壓強項改變為 流體動壓強45 133明槽水流納維斯托克斯方程47 14粘性流動的相似律48 15渦量方程49 第二章納維斯托克斯方程的解58 21平行流動58 211庫埃特流動59 21...
5.7不可壓縮黏性流動的基本特性 5.7.1黏性流動的有旋性 5.7.2黏性流動的旋渦擴散性 5.7.3特性流動的能量耗散性 5.8不可壓縮黏性流體動力學若干解析解 5.8.1平行流動 5.8.2庫埃特流動 5.8.3泊肅葉流動 5.8.4圓管內的...
可求得精確解的最簡單情況是平行流動。這方面有代表性的流動是圓管內的哈根-泊肅葉流動(詳見管流)和兩平行平板間的庫埃特流動(詳見牛頓流體)。在許多情況下,不用解出N-S方程,只要對N-S方程各項作量級分析,就可以確定解的...
4.2 庫埃特流動及其解析解 4.3 庫埃特流動數值解 參考文獻 5 不同雷諾數下非對稱織構承載性能的CFD研究 5.1 引言 5.2 非對稱凹槽織構物理模型 5.3 數值方法及邊界條件 5.3.1 計算模型及幾何參數定義 5.3.2 計算域及邊界...
6.1.1可壓縮流動的基本方程 6.1.2可壓縮層流庫埃特流動 6.1.3激波和激波關係式 6.1.4克羅克定理 6.2可壓縮湍流的統計方程 6.2.1可壓縮湍流運動的系綜平均方程 6.2.2密度加權平均的可壓縮流體運動方程 6.3均勻可壓縮湍流的...
非線性超聲速流的數值解,高超聲速流動基礎理論,牛頓理論等。第4部分(第15~第20章)介紹黏性流動的基本理論及控制方程,庫埃特流動和泊肅葉流動,邊界層特性,層流邊界層和湍流邊界層流動,湍流模型等。本雙語版教材適合相關專業院校...
125無旋流體的流動;從球旁 經過的流動154 126照度;對平面的均勻照明 156 127自然界的“基本統一性”157 第13章靜磁學159 131磁場159 132電流;電荷守恆159 133作用於電流上的磁力161 134恆定電流的磁場;安培...
6.5 庫埃特流動 6.6 流體中的振動板 6.7 蠕動流 6.8 擠壓膜 習題 第7章 電磁學 7.1 電路的基本元件 7.2 基爾霍夫電流定律 7.3 靜電學 7.4 由電場產生的力和力矩 7.5 作用於各種物體的靜電力和力矩 7.6 電磁力 7...
測粘流動 一類特殊的流動。這類流動包括通常在測量流體粘性實驗中所發生的流動。最常見的定常測粘流動有:在兩塊無限平板間的簡單剪下流動;在無限長圓管中的泊肅葉流動;在兩個繞同心軸轉動的圓柱之間流體的庫埃特流動以及圓錐-平板...
[14]胡海豹, 鮑路瑤, 黃蘇和. 不同潤濕性納米通道內庫埃特流動的模擬[J].力學學報,2013,45(4):507-514(EI)[15]胡海豹,陳立斌,黃蘇和. 浸泡法快速製備超疏水黃銅表面[J].上海交通大學學報. 2013,47(8):73-77(EI)[16]...
