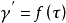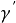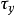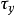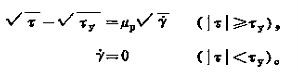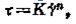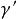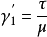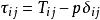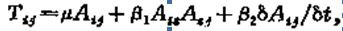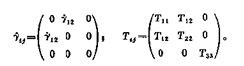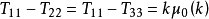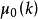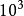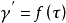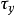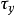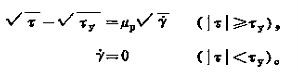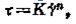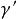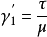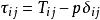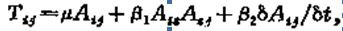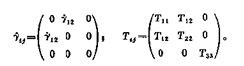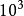基本介紹
- 中文名：非牛頓流體力學
- 外文名：non-Newtonian fluid machanics
- 常見類型：油脂、油漆、牛奶、牙膏
簡史,研究內容,廣義牛頓流體,有時效的非牛頓流體,粘彈性流體,廣義牛頓流體,有時效的非牛頓流體流動,流動穩定性,實驗手段和方法,
簡史
非牛頓流體力學的研究始於1867年J.C.麥克斯韋提出線性粘彈性模型，由於粘彈性流體問題複雜以及當時流體力學大量的研究工作主要集中在牛頓流體方面，所以進展十分緩慢。第二次世界大戰結束後,化學纖維、塑膠、石油等工業的迅速發展，向非牛頓流體力學提出了社會需求;套用數學、流體力學等學科的不斷提高,為非牛頓流體力學提供理論基礎。1950年J.G.奧爾德羅伊德提出建立非牛頓流體本構方程的基本原理，把線性粘彈性理論推廣到非線性範圍。以後，W.諾爾、J.L.埃里克森、R.S.里夫林、C.特魯斯德爾等人對非線性粘彈性理論的發展也作出貢獻。1976年K.沃爾特斯等人創辦國際性專門刊物《非牛頓流體力學雜誌》(Journal of Non-Newtonian Fluid Mechanics)。70年代後期出版了非牛頓流體力學、聚合物加工、流變技術等非牛頓流體力學的專門著作。非牛頓流體力學已發展成為一個獨立的學科。
研究內容
非牛頓流體依照本構方程的不同可分為三類：廣義牛頓流體、有時效的非牛頓流體和粘彈性流體。
廣義牛頓流體
廣義牛頓流體和應力歷史無關的非牛頓流體。自然界中大多數漿糊狀的流體、懸浮液、塑膠熔質等都是廣義牛頓流體。它的本構方程可表示為：
式中
為剪下變形速率；
為剪應力。廣義牛頓流體曲線如圖1所示。下述三種流體都是廣義牛頓流體。
①塑性流體當剪應力低於屈服應力
時，流體靜止並有一定剛度；當剪應力超過 時，流體流動。自然界中含有細砂的懸浮液，以及石油鑽井的泥漿就是這種流體。較常見的塑性流體有賓厄姆塑性（流）體、廣義賓厄姆塑性（流）體和卡森塑性流體。賓厄姆塑性(流)體的本構方程可寫作：
人和牛的血液頗符合卡森方程。
②擬塑性流體：它的粘度隨剪下變形速率的增加而減小。這一特性和擬塑性流體在受剪時趨向於線性結構有關。描述擬塑性流體常用本構方程是：
式中K為模量指數；n為冪律指數,n<1。玉米面糊就是一種膨脹流體。自然界中只有很少的流體是膨脹流體。
有時效的非牛頓流體
有時效的非牛頓流體應力不僅同變形速率而且同時間有關的非牛頓流體，分為觸變流體和觸稠流體兩類。大部分膠狀液體都是觸變流體,其特性是靜止時粘稠,甚至呈固態，攪動後變稀而易於流動。觸變流體在亞微觀狀態下是線性或網狀結構。攪動時，這些結構被破壞，靜止後，它們又重新形成。凝膠漆就是典型的觸變流體。和觸變流體相反，觸稠流體的粘度是隨時間而增加的。這類流體比較稀少，也無工業價值。
有時效的非牛頓流體的本構方程為：
有時效的非牛頓流體的本構方程為：
式中λ(0<λ<)時，結構完全破壞；g(λ，
)在平衡狀態時等於零。μ和g可由實驗確定。
粘彈性流體
粘彈性流體：兼有粘性效應和彈性效應的流體。自然界中許多極粘稠流體(例如瀝青)就是粘彈性流體。粘彈性流體可分為線性粘彈性流體和非線性粘彈性流體。
①線性粘彈性流體 應力和應變及其導數之間呈線性關係的流體。它的粘性效套用牛頓粘性定律描述。剪下變形速率為
，式中μ為動力粘性係數。它的彈性效套用胡克定律描述,剪下變形為
,式中G為剪下模量。總的變形率為
，式中λ=μ/G為鬆弛時間。滿足此本構方程的流體稱為麥克斯韋流體。這種流體可以用一個彈簧和一個粘壺的串聯模型來模擬。實際材料的性質雖然複雜得多，但仍可用一系列的彈簧和粘壺的組合來模擬。
②非線性粘彈性流體 偏應力張量和變形速率張量之間呈非線性關係的流體。
一個流體基元的應力狀態可寫作：
,式中τij為應力張量；Tij為偏應力張量；p為各向同性壓力；δij為克羅內克符號。例如，在大分子溶液和聚合物溶液的定常流動中,當夲增加時,粘度會發生變化,這是由於在流體內每一點上存在各向異性的應力狀態而產生的。非線性粘彈性流體通常有以下幾種模型：二階流體模型、非線性麥克斯韋模型、奧爾德羅伊德三常數模型。二階流體模型的本構方程為：
式中Aij里夫林-埃里克森張量，即變形速率張量的兩倍；δ)/δ)t為牽連導數;β1、β2為材料常數。非線性麥克斯韋模型由線性麥克斯韋模型推廣而得，其本構方程為：
奧爾德羅伊德三常數模型的本構方程為：
式中λ1為鬆弛時間；λ2為材料常數。
此外還有廣義二階流體、三階流體等微分型模型，各種廣義麥克斯韋模型，隱含模型（或稱廣義奧爾德羅伊德模型），積分型模型，根據粘彈性分子理論提出的啞鈴模型、小球-彈簧模型，以及網路模型等等。
廣義牛頓流體
非牛頓流體流動具有與牛頓流體流動截然不同的特性，下面分別簡要說明廣義牛頓流體流動、有時效的非牛頓流體流動、粘彈性流體流動。
廣義牛頓流體流動：塑性流體、膨脹流體和擬塑性流體都是廣義牛頓流體，它們的流動特性是不同的。
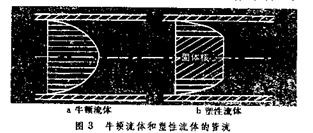
①塑性流體在管中流動時，軸線附近的塑性流體所受的剪應力小於它的屈服應力，因此這種流體類似固體在管中平移；壁面附近的流體則因剪應力超過屈服應力而處於流動狀態。
②擬塑性流體（或膨脹流體）在管道中流動時，流量和壓差的關係是非線性的，而牛頓流體在管道中流動時，這種關係是線性的。
有時效的非牛頓流體流動
以觸變流體為例，若將觸變流體裝入同心圓筒式粘度計的環形縫隙中，則在流體靜止一段長時間後，讓任一圓筒以等速旋轉，就可發現流體的粘度（表現為另一圓筒上的轉矩）隨時間而減小。如果剪下變形速率先不斷增加，後又不斷減小，可以發現觸變流體具有滯回效應。對於不同直徑和長度的管子，流動狀態是不同的，管子越長，管徑越小，觸變現象越明顯。
粘彈性流體流動：粘彈性流體流動是非牛頓流體流動中研究得最為深入的一部分。其典型的流動有：
①定常剪下流動：一種測粘流動，可把它構想為許多層不可伸長的物質面相互之間的滑動。其變形速率和偏應力張量是：
流動由三個材料函式表示:表觀粘度、第一法向應力差係數 和第二法向應力差係數應力差係數。
粘彈性流體的庫埃特流動和泊肅葉流動均屬這種流動。例如在自由面上，粘彈性效應能以外森伯效應的形式表現出來,即粘彈性流體有沿旋轉棒向上爬的傾向。如果把牛頓流體放入容器，它會沿容器壁向上爬升。粘彈性流體從管內自由流出時，通常可以看到射流膨脹現象,這種現象稱為擠出物膨脹。例如，聚苯乙烯在175～200℃條件下較快擠出時,直徑膨脹達2.8倍；而牛頓流體從管中流出時則會收縮。以上現象都是由於粘彈性流體受剪下時產生法向應力差的結果。
②伸長流動：此種流動類似於固體的簡單拉伸。其變形速率和偏應力張量如下：
式中k為伸長應變。而
，
為拉伸粘度,它是k的函式。粘彈性流體拉伸粘度與剪下粘度的比值稱為特勞頓比。對於牛頓流體,這個比值是3；對於粘彈性流體，由於拉伸粘度隨著變形速率增加而增加，這個比值可達到 10～
量級。因此在伸長流動中會產生開口虹吸現象。如果把管子一端插入粘彈性流體，由於虹吸作用，流體經管道流出。如果把插入流體中的管端提出液面,流體仍然會被吸引上來。
在塑膠工業中，大多數加工過程，如纖維拉絲和薄膜吹塑等基本上是伸長流動。滲流和潤滑膜的流動也類似於伸長流動。
③收縮流動：這是介於剪下流動和伸長流動之間的一種複雜流動。在這種流動中，牛頓流體和粘彈性流體也有不同的流場。牛頓流體在中心產生環流，粘彈性流體則在壁面產生環流。塑膠通過一個收縮口被擠入鑄模的流動，聚合物通過噴絲口的流動，大小血管之間血液的流動等都屬於收縮流動。
此外，還有非定常剪下流動等。
流動穩定性
主要研究非牛頓流體定常流動在什麼條件下受到小擾動仍然是穩定的。這方面的研究取得一些成果。在圓筒庫埃特流動中，粘彈性流體的彈性對穩定性影響依賴於所選擇的本構方程和第二法向應力差。若二圓筒的間隙比半徑小很多，當第二法向應力差大於零時,彈性使流動失穩,小於零時正好相反。又如，在大雷諾數下的平面泊肅葉流動（見層流）和斜面流動中，粘性流體的彈性可使流動失穩；在大雷諾數的斜面流動中，粘塑流體的塑性可增加流動的穩定性。另外，在聚合物通過一個收縮口被擠入鑄模的流動中，不穩定流動會使塑膠產品表面產生裂紋。在聚合物的紡絲流動中，不穩定流動除了產生表面裂紋外，還會產生拉絲共振現象，即纖維直徑和法向應力的周期振動。在聚合物加工過程中，小雷諾數流動也會出現不穩定性。流動穩定性的研究，對於化工、化纖、膠片製造等工藝都是十分重要的。
實驗手段和方法
研究和確定非牛頓流體的材料函式和流動特性，常用的主要測試手段有：
同心圓筒式和錐板式旋轉粘度計：它們使試樣產生一均勻的剪下變形速率，通過測量相應的剪下力，直接確定剪應力和剪下變形速率之間的關係，從而算出非牛頓流體的粘度。錐板式粘度計還可測量流體作用在靜止板上的總力，以確定法向應力差。
導管粘度計：通過測量壓力梯度和體積流量，導出剪應力和剪下變形速率之間的關係。它的數據處理比旋轉粘度計複雜，適應性小，但結構簡單並可用作高剪下速率粘度計。此外還有測伸長粘度的伸長流變儀等。
常用的測試方法有：
動態試驗：使材料作正弦變化的剪下運動，跟蹤觀測產生應力的振幅和相位移並作頻率回響分析，可得流體的動態性能。
應力鬆弛試驗：以常速率剪下流體，足夠長時間後流體的流動達定常狀態，再突然停止運動。畫出應力和時間的曲線可確定鬆弛時間。
