簡化函式(reduced function)是在一個子集上不小於一個給定函式的一族函式的下確界。
基本介紹
- 中文名:簡化函式
- 外文名:reduced function
- 適用範圍:數理科學
簡介
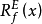
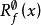
套用
下確界

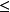









簡化函式(reduced function)是在一個子集上不小於一個給定函式的一族函式的下確界。
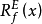
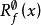

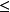









簡化函式(reduced function)是在一個子集上不小於一個給定函式的一族函式的下確界。...
簡化模型(simplified model),也可以稱之為模型簡化,簡單來說是指去掉模型中不顯著的項,通過減少項數使模型更容易使用,或者是指減少模型的複雜度,使模型更容易計算...
目錄 1 牛頓法原理 2 牛頓法運算方法 ▪ 導數法 ▪ 切線法 3 簡化牛頓法 .簡化牛頓法牛頓法原理 編輯 把非線性函式 在 處展開成泰勒級數...
此外,邊摺疊算法還有很好的擴展性。對算法加以改進就可以實現與視點相關的動態簡化。[2]耗散函式V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:5次歷史版本 最近...
數學上的Sgn 函式返回一個整型變數,指出參數的正負號。語法Sgn(number), number 參數是任何有效的數值表達式。返回值如果 number 大於0,則Sgn 返回1;等於0,返回0...
羅斯函式定義為:R=pq·-L。羅斯函式推導 編輯 為了簡化公式,首先假設僅有兩個廣義坐標,用q和ξ表示,現進行從q, ξ, q·,ξ·到q, ξ,p,ξ·的變換,...
基本信息Excel2013新增函式。 本文介紹 Microsoft Excel 中 UNICHAR 函式函式:函式是預先編寫的公式,可以對一個或多個值執行運算,並返回一個或多個值。函式可以簡化...
函式max函式用於求向量或者矩陣的最大元素,或幾個指定值中的最大值。MATLAB等高級程式語言中常用有三種形式:max(A)、max(A,B)、max(A,[],dim)。...
瓦尼爾函式(Wannier function,或沃尼埃函式),是固體物理學中的一個正交函式的完備集,由格里高利·瓦尼爾提出。瓦尼爾函式在晶系中對應著局域化分子軌道。晶體中不同...
SHEET是函式函式:函式是預先編寫的公式,可以對一個或多個值執行運算,並返回一個或多個值。函式可以簡化和縮短工作表中的公式,尤其在用公式執行很長或複雜的計算...
階躍函式是一種特殊的連續時間函式,是一個從0跳變到1的過程,屬於奇異函式。在電路分析中,階躍函式是研究動態電路階躍回響的基礎。利用階躍函式可以信號處理、積分...
一般地,對數函式以冪(真數)為自變數,指數為因變數,底數為常量的函式。對數函式是6類基本初等函式之一。其中對數的定義:如果ax=N(a>0,且a≠1),那么數x...
Matlab Mupad 命令。命令Simplify(expr)簡化表達式,注意:S大寫。(expr為表達式)...... 命令Simplify(expr)簡化表達式,注意:S大寫。(expr為表達式)中文名 Simplify函...
素函式(prime function)是函式分解論中一類具特殊性質的函式。設F(z)為一亞純函式,若F的任一個分解式f°g中,必導致f或g為一雙線性函式時,則稱F為素函式。...
損失函式(loss function)或代價函式(cost function)是將隨機事件或其有關隨機變數的取值映射為非負實數以表示該隨機事件的“風險”或“損失”的函式。在套用中,...
生產函式可以用一個數理模型、圖表或圖形來表示。”生產”在經濟學中是一個具有普遍意義的概念,經濟學意義上的“生產“不僅僅意味著制查一台工具機或是紡織一匹布,...
信號處理專題的優秀論文,包括數字濾波、信號與頻譜分析、高速函式逼近、信號生成和...它們可以簡化一般的信號處理過程,或者提高信號處理的計算速度,能夠為DSP工程師們...
卡諾圖化簡法(reduced method of a Karnaugh map)是化簡真值函式的方法之一,它具有幾何直觀性這一明顯的特點,在變元較少(不超過六個)的情況下比較方便,且能...
梯度下降法實現簡單,當目標函式是凸函式時,梯度下降法的解是全局解。一般情況下...Hessian矩陣的逆矩陣的缺陷,它使用正定矩陣來近似Hessian矩陣的逆,從而簡化了運算...
最最佳化方法,是指解決最最佳化問題的方法。所謂最最佳化問題,指在某些約束條件下,決定某些可選擇的變數應該取何值,使所選定的目標函式達到最優的問題。即運用最新科技...
