卡諾圖化簡法(reduced method of a Karnaugh map)是化簡真值函式的方法之一,它具有幾何直觀性這一明顯的特點,在變元較少(不超過六個)的情況下比較方便,且能得到最簡結果。此法由卡諾(M.Karnaugh)於1953年提出,其具體步驟如下:1.構造卡諾框;2.在卡諾框上做出所給真值函式f的卡諾圖;3.用卡諾圖化簡真值函式,首先把相鄰的1字塊兩兩合成矩形得到一維塊;把22個相鄰的1字塊合成矩形(或正方形)得到二維塊;把23個相鄰的1字塊合成矩形得到三維塊等,合成的各種維塊統稱f的合塊;4.把f的卡諾圖中全部1字塊做成若干個合塊,這樣一組合塊就稱為f的一個覆蓋組,f的一切覆蓋組中所含塊數最小的組即是f的最小覆蓋組;5.在最小覆蓋組中,合塊維數總和最大的組的對應式是f的最簡式。
基本介紹
- 中文名:卡諾圖化簡法
- 外文名:reduced method of a Karnaugh map
- 所屬學科:數學
- 簡介:化簡真值函式的方法之一
- 提出者:卡諾(M.Karnaugh)
基本介紹
卡諾圖的構成
基本原理
構圖
 圖3 四變數卡諾圖
圖3 四變數卡諾圖邏輯函式在卡諾圖上的表示
卡諾圖化簡邏輯函式的原理
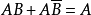
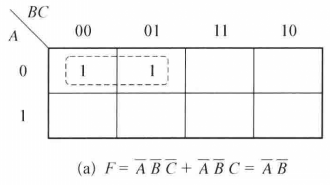 圖4(a)
圖4(a)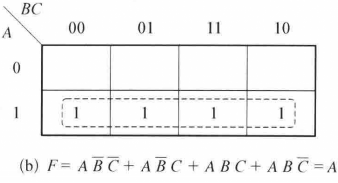 圖4(b)
圖4(b)例題解析
 圖5
圖5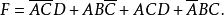
 圖6
圖6
