卡諾框

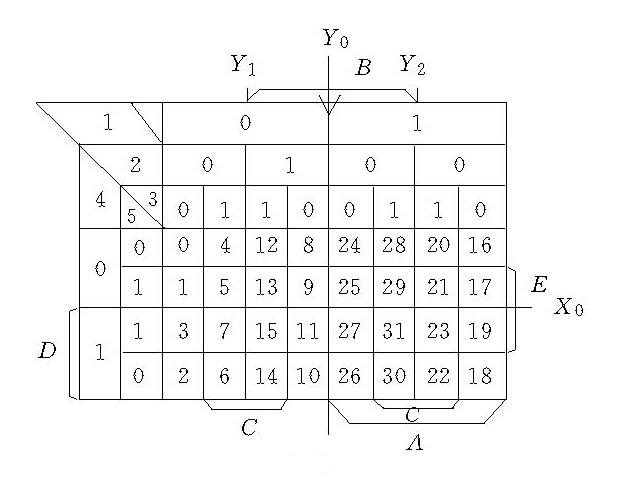
卡諾框(Karnaugh block)是卡諾圖化簡法中的步驟之一，把一個矩形分成小方格，使每一個小方格表示一個極小項，這樣的矩形稱為卡諾框。

基本介紹

• 中文名：卡諾框
• 外文名：Karnaugh block
• 所屬學科：數學（布爾代數）
• 簡介：卡諾圖化簡法中的步驟之一

基本介紹

把一個矩形分成小方格，使每一個小方格表示一個極小項，這樣的矩形稱為卡諾框。由於n個變元的一切可能的最小項有2ⁿ個，所以n元的卡諾框具有2ⁿ個小方格，當n為偶數時，卡諾框呈正方形，否則呈長方形，r個不同字的乘積一般用所謂坐標架法來構造卡諾框，圖中給出三至五元的卡諾框的三個結構(在圖2、圖3的小方格中用10進位數代替二進位數)，A₁A₂…A_r(1≤r≤n)稱為小項，其中每個字分別是變元x₁，x₂，…，x_n中某個變元或變元的補，極小項顯然是小項，兩個小項中，如果一項有一個字與另一項的同位字互相否定，而其他的字完全相同，則稱這兩個項互為鄰項，如果兩極小項互為鄰項，則稱卡諾框中表示這兩項的小格互為鄰格，鄰格在框圖中是有公共邊的或關於某個軸對稱的兩個小格，卡諾框中的各小格稱為0維塊，兩個相鄰的0維塊合併成一個一維塊，兩個相鄰的一維塊的對應項仍為鄰項，二者合併成一個二維塊等。

圖1

圖2

圖3

相關介紹

簡單說來，卡諾(Karnaugh)圖就是開關函式1值標準形的幾何圖。為什麼能畫出1值標準形的幾何圖，這是因為集代數有相應的幾何圖，而集代數與開關代數的運算、基本定律等又都是一一對應的，因此可以用集代數的幾何圖表示開關代數：用子集A、B表示開關變數A、B，用交集AB表示輸入端為么與B的與門的輸出，用補集A’表示輸入端為A的非門的輸出，如此等等。

1值標準形是由某些小項組成的，要能畫出1值標準形的圖，首先要畫出小項的圖，為此，可將開關變數都畫成矩形，A、B二個變數時彼此按如下方式迭蓋起來：

圖4(a)

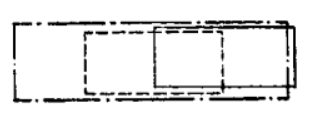圖4(b)

如果是A、B、C三個開關變數就按如下方式迭蓋：

圖5(a)

圖5(b)

為了畫圖的簡便，圖5中的右圖可簡畫如下：

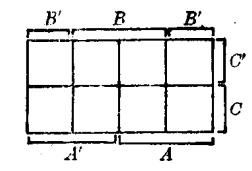圖6

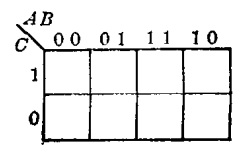圖7

如此畫出的框(圖6及圖7)叫卡諾框。

圖6與圖7的不同只是表面上的，因為經過如下的演變，圖6就變成圖7了：

卡諾框的作用類似於解析幾何中的坐標架，若將圖7中的：

00，01，11，10

看作橫坐標，而將

0，1

看作縱坐標，則將二者結合起來(橫坐標在左，縱坐標在右)，就得圖9中的每一格中的二進位數；將這些二進位數寫成對應的十進位數，就是圖10。

這樣，卡諾框的每一小格都對應於一個小項：圖9中每一小格的二進位數，就是這些格對應小項的指向量.例如，第011格就對應於小項

這一點，從圖6也不難看出,卡諾框的每一小格所對應的小項.例如，圖11中的第6格(110)，它同屬於A、B及C’故應是小項ABC’；而其中的第3格(011)則同屬於A’、B及C，故應是小項A’BC．將這些小項全寫出來，就是圖12(由圖8中的(b)可以更容易地寫出圖12)，請注意卡諾框的一個重要性質：二個相鄰格的小項，有且僅有一個因子不同，而且這一個不同的因子是互補的。

因為每一個開關函式都可唯一地表成標準形，所以當要圖示f時，可先把f寫成標準形。例如把

寫成

然後畫一個卡諾框，在與1值小項對應的格中寫上1就行(圖13)，這種寫上1值的卡諾框就是對應開關函式的卡諾圖。

圖13