等邊對等角是三角形的一種,在同一三角形中,兩條邊相等,則兩個邊的對角相等,即等邊對等角,如等腰直角三角形,是等角對等邊的逆定理(這是公理)。
基本介紹
- 中文名:等邊對等角
- 外文名:無
- 如:等腰直角三角形
- 限制:在同一三角形中
證明方法
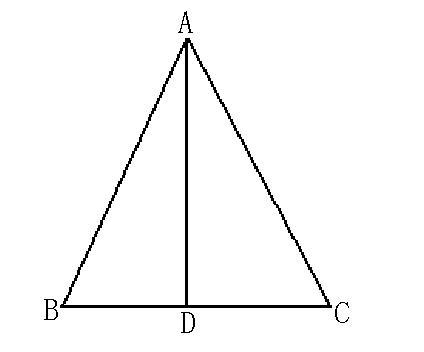 等邊對等角證明
等邊對等角證明
等邊對等角是三角形的一種,在同一三角形中,兩條邊相等,則兩個邊的對角相等,即等邊對等角,如等腰直角三角形,是等角對等邊的逆定理(這是公理)。
 等邊對等角證明
等邊對等角證明等邊對等角是三角形的一種,在同一三角形中,兩條邊相等,則兩個邊的對角相等,即等邊對等角,如等腰直角三角形,是等角對等邊的逆定理(這是公理)。...
對角,是指在三角形中兩邊所夾的內角稱為第三邊的對角。對角的套用:1、等邊對等角:等腰三角形中,相等的兩腰的對角也相等。2、等角對等邊:三角形中如果兩個...
他一生髮現了多個幾何學定理,包括等腰三角形中的“等邊對等角”定理,也包括對頂角定理。對頂角對頂角定理 編輯 設直線AD、BC交於點O,那么,∠AOB和∠AOC 互為...
則因DA = AC ,∠ADC = ∠ACD (等邊對等角,《幾何原本》命題5)所以∠BCD大於∠ADC(平行公設)由於DCB是三角形,∠BCD大於∠BDC,而且較大角所對的邊較大(...
1.等腰三角形的兩個底角度數相等(簡寫成“等邊對等角”)。2.等腰三角形的頂角平分線,底邊上的中線,底邊上的高相互重合(簡寫成“等腰三角形三線合一”)。...
∵AD=CD∴∠A=∠ACD(等邊對等角)∵∠A+∠B=90°(直角三角形兩銳角互余),∠ACD+∠BCD=∠ACB=90°∴∠B=∠BCD(等角的餘角相等)∴BD=CD(等角對等邊)...
1.等腰三角形的兩個底角度數相等(簡寫成“等邊對等角”)。 2.等腰三角形的頂角平分線,底邊上的中線,底邊上的高相互重合(簡寫成“等腰三角形三線合一”)。 3....
則∠D=∠ACD(等邊對等角)∵∠BCD>∠ACD∴∠BCD>∠D∴BD>BC(大角對大邊)∵BD=AB+AD=AB+AC∴AB+AC>BC三角形的關係 一般三角形設三角形三邊為AC,BC,AB...
1.等腰三角形的兩個底角相等。 (簡寫成“等邊對等角”)2.等腰三角形的頂角的平分線,底邊上的中線,底邊上的高的重合(簡寫成“三線合一”)...
∴∠CAB=∠CBA(等腰三角形中等邊對等角)例題2 【例2】如圖,AD是ΔABC中∠BAC的平分線,經過點A的圓與BC相切於點D,與AB,AC分別相交於E,F....
等腰三角形的兩個底角度數相等(簡寫成“等邊對等角”)。等腰三角形的頂角的平分線,底邊上的中線,底邊上的高重合(簡寫成“等腰三角形的三線合一性質”)。等腰三角...
注意到上述證明過程中,藉助了“等腰三角形等邊對等角”這一定理,儘管課標對“邊邊邊”不作證明要求,但從幾何定理的編排順序以及數學教材的嚴謹性來講,在呈現“邊...
29 角的平分線是到角的兩邊距離相等的所有點的集合30等腰三角形的性質定理 等腰三角形的兩個底角相等 (即等邊對等角)31 推論1 等腰三角形頂角的平分線平分底邊...
有些參考資料提到法國和比利時將勾股定理稱為驢橋定理,但驢橋定理就是等邊對等角,是指等腰三角形的二底角相等,非勾股定理。即在平面上的一個直角三角形中,兩個...
