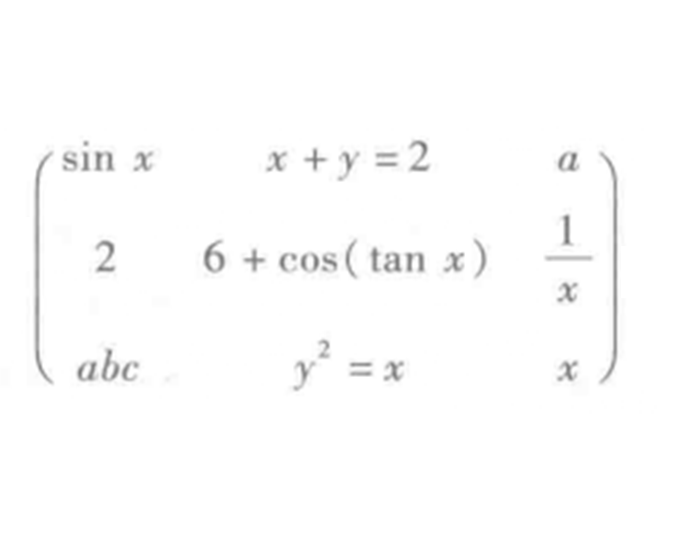符號矩陣

符號矩陣是一種由四個符號學要素組成的顯示的矩形圖式。它是一種不同於數值矩陣的特殊的符號表達式，數值矩陣不能參與符號運算，若要參與的話，應該首先轉化為符號矩陣。符號矩陣的運算包括：加（+）、減（-）、乘（×）、除（/、\）、轉置（'）、行列式（det）、逆（inv）、秩（rank）、冪（^）等。

基本介紹

• 中文名：符號矩陣
• 外文名：Symbolic matrix
• 組成部分：四個符號學要素
• 性質：矩形圖式
• 提出者：格雷馬斯
• 套用學科：高等數學、數學實驗

定義

符號矩陣是一種特殊的符號表達式，MATLAB中的符號矩陣可以通過sym函式來建立，矩陣的元素可以是任何不帶符號的符號表達式，其調用格式是：

符號矩陣名=sym('符號字元串矩陣')

符號字元串矩陣的各元素之間可以用空格或逗號分隔。在MATLAB中，數值矩陣不能直接參與符號運算，必須先轉換為符號矩陣，同樣也是通過sym函式來轉換。

運算

基本運算

符號矩陣的四則運算與數值矩陣有完全相同的運算方式，其運算符為：加（+）、減（-）、乘（×）、除（/、\）等。

特殊運算

符號矩陣還可以進行如下運算：轉置（'）、行列式（det）、逆（inv）、秩（rank）、冪（^）等。

相關操作

生成

A=sym('[aa,bb;1,a+2*b]')

運行程式輸出結果得：

A=     [aa,  bb]     [1,a+2*b]

逆

>>inv(A)=                  [(a+2*b)/(a*aa-bb+2*a*b),-bb/(a*aa-bb+2*a*b)]                 [  -1/(a*aa-bb+2*a*b), aa/(a*aa-bb+2*a*b)]

秩

>>rank(A)ans=        2

符號矩陣的上三角

>>triu(A)ans=        [aa,  bb]        [0,a+2*b]

符號矩陣的下三角

>>tril(A)ans=        [aa,   0]        [1,a+2*b]

數值矩陣轉換為符號矩陣

在MATLAB中，必須事先定義符號矩陣，才能對矩陣進行符號運算，將數值矩陣轉換成符號矩陣的調用格式為：

sym(矩陣名)：數值矩陣轉換成符號矩陣

例如：

>>A=hilb(3)>>A=sym(A)

運行結果如下：

A=   1.0000    0.5000    0.3333   0.5000    0.3333    0.2500   0.3333    0.2500    0.2000A=   [1  ,1/2,1/3]   [1/2,1/3,1/4]   [1/3,1/4,1/5]