基本介紹
- 中文名:空間曲線
- 外文名:Space curve
- 存在空間:三維歐式空間
- 套用領域:經典微分幾何
- 基本要素:弧長、曲率和撓率
- 研究工具:微積分
介紹
 DNA的雙螺旋結構
DNA的雙螺旋結構表示式
參數方程
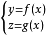


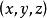
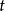
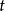

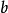
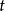

向量方程




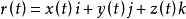
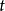
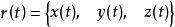
三個元素
弧長
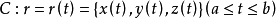
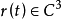


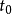
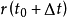





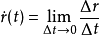

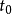
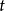

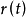
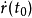
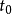



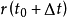
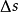
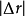
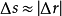
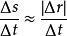


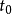
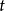



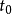
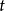
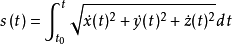
曲率

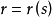

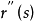




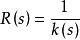

撓率





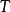


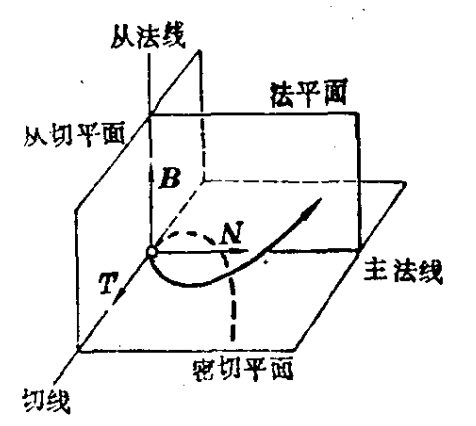


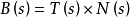
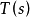

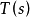


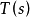

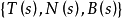



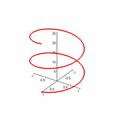
 DNA的雙螺旋結構
DNA的雙螺旋結構


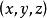
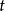
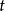

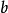
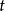





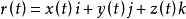
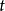
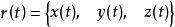
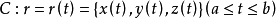
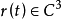


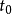
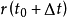





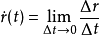

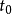
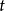

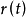
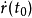
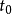



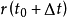
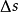
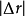
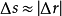
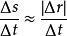


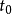
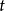



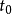
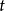
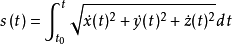

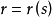

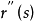




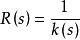






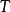





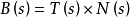
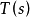

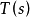


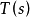

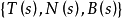



空間曲線(space curves)是經典微分幾何的主要研究對象之一,在直觀上曲線可看成空間一個自由度的質點運動的軌跡。研究空間曲線的有力工具是微積分,我們可以用微積分...
希爾伯特曲線是一種奇妙的曲線,只要恰當選擇函式,畫出一條連續的參數曲線,當參數t在0,1區間取值時,曲線將遍歷單位正方形中所有的點,得到一條充滿空間的曲線。 ...
空間的兩條直線有以下三種位置關係:1.相交直線,2.平行直線,3.異面直線。...... 空間的兩條直線有以下三種位置關係:1.相交直線,2.平行直線,3.異面直線。 ...
維維安尼曲線是以義大利數學家維維安尼命名的由特定球面與圓柱相交形成的曲線。...... 2的圓柱面相交而成的空間曲線(如圖),它是以義大利數學家維維安尼的名字命名的曲...
“曲線坐標”是天文學專有名詞。曲線坐標計算程式可計算圓曲線帶有緩和曲線、邊樁坐標及切線方位角,附有正算、反算功能。正算:通過里程和偏距計算坐標;反算:通過...
定義在平面曲線或空間曲線上的函式關於該曲線的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲線,計算該曲線的質量。...
直觀上,富勒氏曲線可看成空間質點運動的軌跡。曲線的更嚴格的定義是區間【α,b)】到E3中的映射r:【α,b)】→E3。有時也把這映射的像稱為曲線。具體地說,設...
在數學中,平面曲線是可以是歐幾里德平面、仿射平面或投影平面中的曲線。 最常研究的情況是平滑平面曲線(包括分段平滑曲線)和代數平面曲線。...
我們把所有虧格g的光滑代數曲線--在同構意義下--放在一起構成的集合。該集合形成一個擬代數簇, 我們稱它為虧格g曲線模空間, 記為Μ_g。 一般說來, M_g不...
空間羅倫茲曲線 , 是用以對比分析空間分布的集散狀態。...... 空間羅倫茲曲線 , 是用以對比分析空間分布的集散狀態。它是研究離散區域分布的一種重要方法。羅倫茲...
皮亞諾曲線(Peano曲線)是一曲線序列的極限,不再是通常定義下的曲線。下文中“曲線”應解釋為“曲線的極限”。只要恰當選擇函式,畫出一條連續的參數曲線,當參數t...
定向曲線(oriented curve)亦稱有向曲線,指規定了方向的曲線。對曲線Γ:x=φ(t),t∈[a,b]可以按參數增加(或減少)規定Γ的方向,即規定t₁<t₂(或t₂<...
對於滿足一些條件的曲線,起點和終點的位置固定,沿不同的路線積分,其積分值相同,即曲線積分只與起點和終點有關,與路線的選取無關。...
遺忘曲線由德國心理學家艾賓浩斯(H.Ebbinghaus)研究發現,描述了人類大腦對新事物遺忘的規律。人體大腦對新事物遺忘的循序漸進的直觀描述,人們可以從遺忘曲線中掌握遺忘...
在直角坐標系中,如果某曲線C上的點與一個二元方程f(x,y)=0的實數解建立了如下的關係:(1)曲線上點的坐標都是這個方程的解;(2)以這個方程的解為坐標的點...
