空間折線(space broken line)是一種空間圖形,依次首尾相接的若干線段組成的空間圖形稱為空間折線。組成空間折線的各線段,可以不共面。
基本介紹
- 中文名:空間折線
- 外文名:space broken line
- 所屬學科:數學
- 所屬問題:空間幾何
- 簡介:依次首尾相接的若干線段
基本概念
 圖1
圖1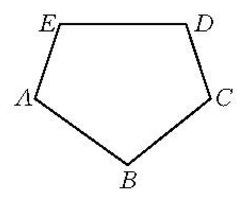 圖2
圖2相關結論
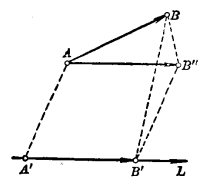 圖3
圖3







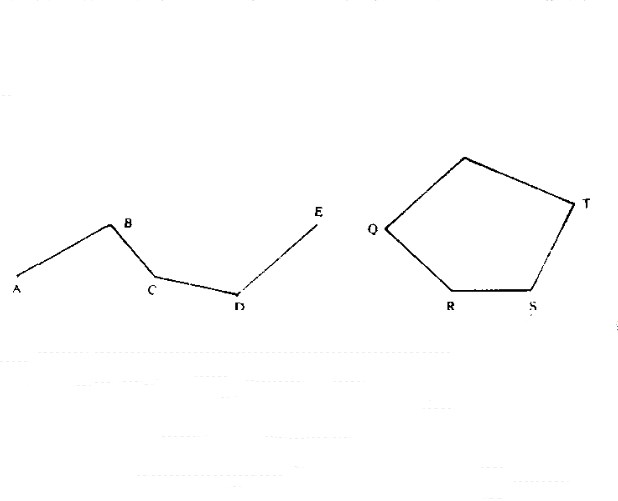
空間折線(space broken line)是一種空間圖形,依次首尾相接的若干線段組成的空間圖形稱為空間折線。組成空間折線的各線段,可以不共面。
 圖1
圖1 圖2
圖2 圖3
圖3







空間折線(space broken line)是一種空間圖形,依次首尾相接的若干線段組成的空間圖形稱為空間折線。組成空間折線的各線段,可以不共面。...
空間曲線(space curves)是經典微分幾何的主要研究對象之一,在直觀上曲線可看成空間一個自由度的質點運動的軌跡。研究空間曲線的有力工具是微積分,我們可以用微積分...
折線指的是多條線段首尾依次相接組成的曲折連線,也可以說折線是把不在一條直線上的幾個點(稱為端點),依次用線段連線起來(每個公共端至多有兩條線段相連)所構成...
封閉折線是一種幾何圖形,指一種特殊的折線。同一平面內,由不在同一直線上的幾條線段順次首尾相接所組成的圖形叫作折線,如果一條折線的首尾兩個端點重合,這條...
空間多邊形(Spacial polyhedron)亦稱捩多邊形,是一種空間圖形,常指各邊不共面的多邊形。不在同一平面內的若干線段首尾相接所成的圖形叫做空間折線;若空間折線的最後...
折線筆畫輸入法根據每個折線段的方向角度進行分類,並建立起每類折線與輸入字元之間的對應關係。在用戶劃出特定類型的折線筆畫後,系統根據折線各線段的方向角度判定出...
空間羅倫茲曲線 , 是用以對比分析空間分布的集散狀態。...... 空間羅倫茲曲線 , 是用以對比分析空間分布的集散狀態。它是研究離散區域分布的一種重要方法。羅倫茲...
我們把所有虧格g的光滑代數曲線--在同構意義下--放在一起構成的集合。該集合形成一個擬代數簇, 我們稱它為虧格g曲線模空間, 記為Μ_g。 一般說來, M_g不...
空間桁架,即球節架,屬於輕便剛性結構構造組成一個幾何樣式。球節架通常運用一個多向間距,是由張力桿和壓力桿組成的結構,結構處在三度空間的受力狀態下,無論哪...
空間曲線 目錄 1 基本介紹 2 平滑曲線 3 代數曲線 4 舉例 平面曲線基本介紹 編輯 在數學中,平面曲線是可以是歐幾里德平面、仿射平面或投影平面中的曲線。 ...
撓率,它的絕對值度量了曲線上鄰近兩點的次法向量之間的夾角對弧長的變化率。平面曲線是撓率恆為零的曲線。空間曲線如不是落在一平面上,則稱為撓曲線。在三維曲線...
維維安尼曲線是一個半徑為a的球面與一個經過球面的一條直徑,且半徑為a/2的圓柱面相交而成的空間曲線(如圖),它是以義大利數學家維維安尼的名字命名的曲線。...
如空間定向曲線 的參數方程為則 的切向量為又如平面定向曲線L的方程為 ,則該定向曲線的切向量為若定向曲線L的方程為 ,則其切向量為 [2] ...
希爾伯特曲線是一種奇妙的曲線,只要恰當選擇函式,畫出一條連續的參數曲線,當參數t在0,1區間取值時,曲線將遍歷單位正方形中所有的點,得到一條充滿空間的曲線。 ...
定義在平面曲線或空間曲線上的函式關於該曲線的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲線,計算該曲線的質量。...
1890年,義大利數學家皮亞諾(G.Peano)構造了填充空間的曲線。該曲線即為Peano填充曲線。...
空間曲線坐標系,由空間曲面組(坐標曲面)的交線確定。如圖1,三維情況:y1=const.確定一曲面,稱為y1曲面;y2=const.,y3=const.分別為y2,y3曲面。在y2曲面和y3...
曲線,是微分幾何學研究的主要對象之一。直觀上,曲線可看成空間質點運動的軌跡。微分幾何就是利用微積分來研究幾何的學科。為了能夠套用微積分的知識,我們不能考慮...
