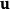基本介紹
- 中文名：稠密光流
- 外文名：Dense Optical Flow
- 領域：計算機視覺
- 套用：圖像配準
方法介紹,函式與求解,L2-光流,L1-光流,求解,解析解項,
方法介紹
稠密光流是一種針對圖像進行逐點匹配的圖像配準方法，不同於稀疏光流只針對圖像上若干個特徵點，稠密光流計算圖像上所有的點的偏移量，從而形成一個稠密的光流場。通過這個稠密的光流場，可以進行像素級別的圖像配準，所以其配準後的效果也明顯優於稀疏光流配準的效果。但是其副作用也是明顯的，由於要計算每個點的偏移量，其計算量也明顯大於稀疏光流。
函式與求解
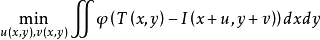
上式中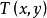
為參考圖像（第一張圖像），
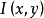為當前圖像（第二張圖像），也是待配準圖像。偏移量
是圖像上每一點的偏移量，
是一個誤差函式，根據不同的需求可以取絕對值函式，二次函式等一些非負對稱且正半軸單調遞增的函式。
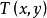
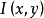
由於是稠密匹配，如果單一隻有上面的數據項是不夠的，因為對純色區域的點顯然是沒法通過上式找到準確的偏移量的，因此還需要加入一個平滑項。平滑項的目的就是，對於特徵比較弱的區域的點，其偏移量儘量向強特徵點的偏移量靠近，或者說相鄰兩個特徵點的偏移量相差不能太大，也就是偏移量的變化率不能太大，用數學語言描述就是：
上式中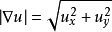
是梯度的模長，
是一個類似 的誤差函式。
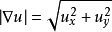
將上面兩個公式合併起來就得到了最終的目標函式：
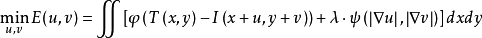
為了描述簡單，上面的偏移量 就不寫成顯著的函式形式，
是一個權重因子。目前主流的稠密光流算法中，主要根據誤差函式取絕對值函式和二次函式分成兩大類（其他函式由於複雜度較高，一般比較少討論）：L1-光流（L1-範數）和L2-光流（L2-範數）。下面就兩大類光流進行討論：
L2-光流
L2-光流是最早進行研究的稠密光流，由於其兩個誤差函式都是二次函式，因此被稱為L2-光流。由於二次函式是所有誤差函式中最容易進行極值求解的，因此這種方法在快速計算中經常被用到。L2-光流最早是Horn和Schunck在1981年提出並求解的，因此也被稱為H-S算法。
L2-光流的目標函式如下：
將上面的定積分形式改寫成離散的形式：
其中：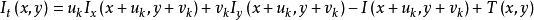
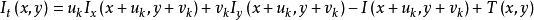
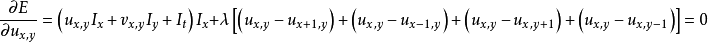
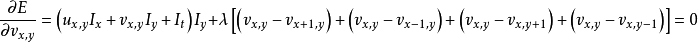
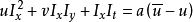
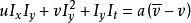
上式中：
，
，
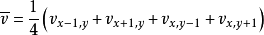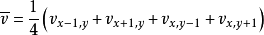
Lluís Garrido提供了HS-算法的c語言實現。
L1-光流
相對於L2-光流，L1-光流提出的時間就相對要晚很多了，具體原因可能是其求解過程比較複雜。但是採用L1-範數有個好處是，誤差函式增長較慢，這樣對於大的偏移量的懲罰項也相對較小，從而可以計算偏移量較大的光流。其目標函式的數據項和平滑項由兩個絕對值函式組成，因此被稱為L1-光流。具體目標函式如下：
由於絕對值函式在0點處沒有導數，因此一般不適合傳統導數方法求極值。有一種近似做法是採用另一個處處可微的函式替代絕對值函式：
其中s是一個非常小的常數，這樣就可以採用傳統的梯度法和牛頓法對上面的函式進行極值求解了。唯一的不足是，採用上面的近似後，導數的計算較為複雜，每次疊代的計算量灰常大，計算速度很慢。後來有一個哥們發現數學上有個Total Variation（TV）可以用於二次式與絕對值和的求解，因此又整出了一套稱為TV-L1的高大上的解法，這種解法相對上面的解法的優點就是快，另外也更精確。正因為如此，後面發論文的也基本都採用L1-範數的形式。
TV-L1的基本思想就是把目標函式拆分成兩個：一個標準TV-L1的形式，另一個可以直接求解析解的形式。為了方便書寫，將二元組
用向量
表示，
用向量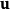
表示，引入輔助變數
，目標函式可以簡寫為：
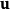
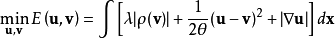
其中：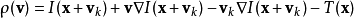
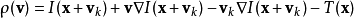
然後將其拆分成標準的TV-L1形式：
和可直接求解析解項：
其求解過程採用螺旋法。
求解
首先固定
，然後採用TV-L1求解第一項中的
可以得到：
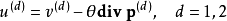
其中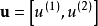
，
，
由下面的疊代式計算：
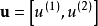
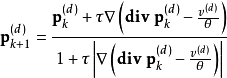
其中
，初始值
，疊代步長
解析解項
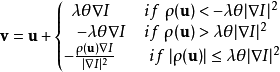
求出
後將其代回1中繼續求解
，直到
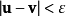終止疊代。
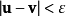
opencv2.3裡面有TV-L1的原始碼實現，可以參考其原始碼理解算法流程。
