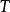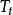基本介紹
- 中文名:稀疏光流
- 外文名:Sparse Optical Flow
- 領域:計算機視覺
- 套用:圖像配準,目標跟蹤
定義,目標函式,標準解法,逆向解法,
定義
稀疏光流是一類專門針對圖像上稀疏的點進行圖像配準的方法,也就是在參考圖上給定若干個點(一般為角點),找到其在當前圖像中的對應點。用數學的語言描述就是,給定參考圖T和當前圖I,計算參考圖T中的一個角點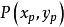 在當前圖I中對應的點
在當前圖I中對應的點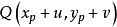 ,其中
,其中 就是角點的偏移量。如果以當P點和Q點為中心的兩個小矩形視窗內的所有點都相同,那么就表示這兩個點是匹配的。
就是角點的偏移量。如果以當P點和Q點為中心的兩個小矩形視窗內的所有點都相同,那么就表示這兩個點是匹配的。
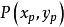
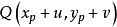

目標函式
在實際的圖像數據中,由於有噪聲的存在,兩個對應點所在的小矩形視窗內的像素點不可能完全相同,因此可以考慮取其差異最小的一個位置為匹配點,也就求解如下目標函式:
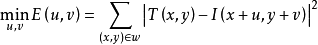
其中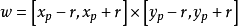 是一個以
是一個以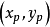 為中心,
為中心, 為半徑的矩形視窗。
為半徑的矩形視窗。
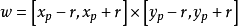
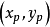

標準解法
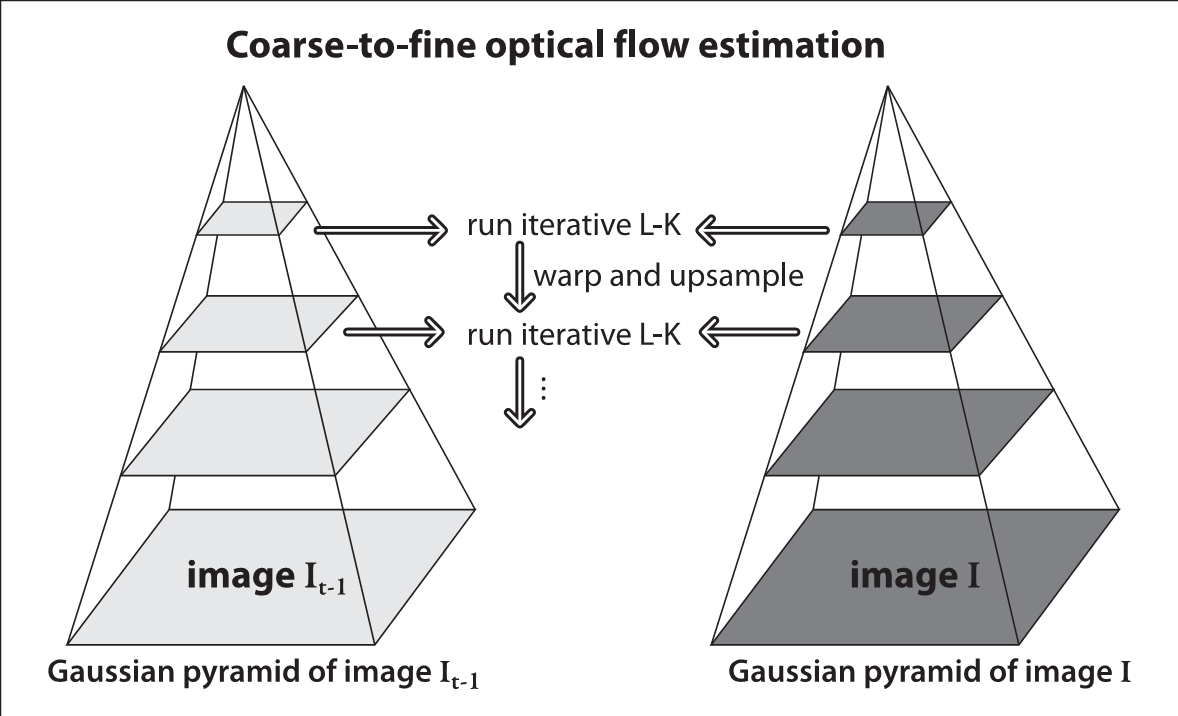
上式可以用非線性最小二乘法進行求解,為了加速同時也為了計算大偏移量,一般使用圖像金字塔的方法來求解。其基本思想就是在小圖上先算出一個初始值,然後將這個初始值乘2作為下一層的初始值,這樣每層只需要疊代很少的步驟就可以收斂。具體計算每一層使用的算法是高斯牛頓法,具體做法如下:
將後一項進行一階Taylor展開得到:
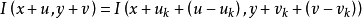


將上式帶入目標函式可以得到:
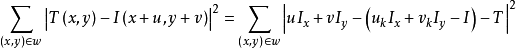
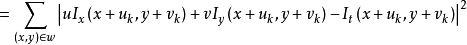
其中: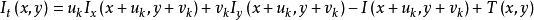
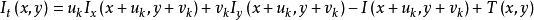
對 求偏導數可以得到:
求偏導數可以得到:

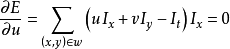
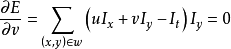
為了書寫方便,重新定義以下符號:

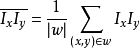

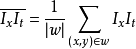

由此不難得到二元一次方程組:
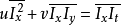
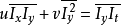
解出 即可得到偏移量。
即可得到偏移量。



根據柯西不等式, 恆成立,只有當兩向量平行時才會取到等號,此時對應的圖像為純色或者只有單一的直線邊緣,因此一般要求特徵點為角點,這樣可以保證分母恆大於0.
恆成立,只有當兩向量平行時才會取到等號,此時對應的圖像為純色或者只有單一的直線邊緣,因此一般要求特徵點為角點,這樣可以保證分母恆大於0.

逆向解法
以上的解法為Lucas–Kanade光流(簡稱LK光流)的標準流程,由於在第一步做Taylor展開的時候,針對的是當前圖像 ,而待求變數
,而待求變數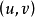 也在
也在 中,因此也被稱為正向解法。這種求解方法比較直接,但是在疊代計算的時候每次都需要重新對梯度圖像進行插值計算,算法性能較慢。
中,因此也被稱為正向解法。這種求解方法比較直接,但是在疊代計算的時候每次都需要重新對梯度圖像進行插值計算,算法性能較慢。

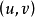

針對上面的問題,Baker提出了一種逆向混合算法,其基本思想就是將增長變數與疊代變數分別置於兩個函式中,這樣對增長變數做Taylor近似的時候,其所在的函式不含有疊代變數,因此疊代的過程中不需要重新插值計算梯度圖像。
考察目標函式中的誤差函式:

上式中 為疊代變數,
為疊代變數, 為增長變數,用
為增長變數,用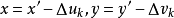 進行變數替換可以得到:
進行變數替換可以得到: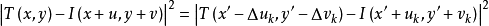 ,由於每次的增長量
,由於每次的增長量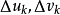 比較小,所以可以近似認為變換後的求和區間沒有變化,也就是
比較小,所以可以近似認為變換後的求和區間沒有變化,也就是 ,因此可以將原始目標函式寫為如下形式:
,因此可以將原始目標函式寫為如下形式:


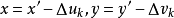
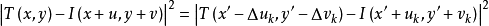
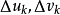


採用高斯牛頓法可以得到最終的二次形式:

其中: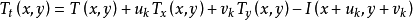
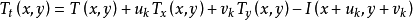
對 求偏導數可以得到:
求偏導數可以得到:



由此可以解出 得到:
得到:


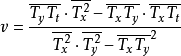
不難看出,上面的公式與標準解法的公式非常相似,僅僅是把 換成了
換成了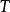 ,但還有一個隱含的不同點,那就是計算平均值的時候,標準算法是對
,但還有一個隱含的不同點,那就是計算平均值的時候,標準算法是對 的求和,這樣每次疊代的時候都需要重新對梯度圖像進行插值計算;而逆向算法是對
的求和,這樣每次疊代的時候都需要重新對梯度圖像進行插值計算;而逆向算法是對 的求和,與
的求和,與 無關,因此在疊代的過程中除了含有
無關,因此在疊代的過程中除了含有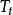 的項需要重新計算,其他項都是不變的,這樣可以大大的減少計算量。
的項需要重新計算,其他項都是不變的,這樣可以大大的減少計算量。