秦九韶方法

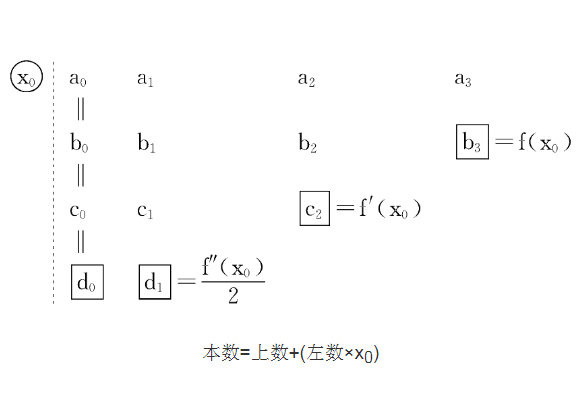
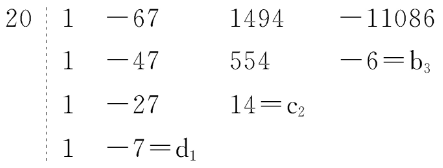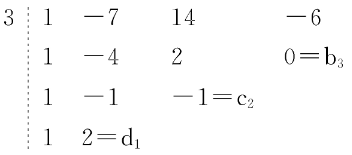秦九韶方法(Qin Jiushao method)是求實係數多項式實根近似值的一種方法。例如，設實係數多項式f(x)在[3，4]內有一實根α，令x=3+y，即y=x-3，再令f₁(y)=f(3+y)，則f₁(y)在[0，1]內有一個相應的實根，把[0，1]分為十個小的區間[0，0.1]，[0.1，0.2]，…，[0.9，1]，看f₁(y)的相應實根在哪個區間內，比如在[0.7，0.8]內，令y=0.7+z，z=y-0.7，設f₂(z)=f₁(0.7+z)，則f₂(z)在[0，0.1]內必有相應的一個實根，同樣，把[0，0.1]分成十個小區間[0，0.01]，[0.01，0.02]，…，[0.09，0.1]，看f₂(z)的相應實根在哪個區間內，比如在[0.04，0.05]內，於是α∈[3.74，3.75]，則3.74與3.75就是f(x)的實根α精確到0.01的近似值，前者是不足近似值，後者是過剩近似值，如此下去，可達到所需要的精確度。這個方法是秦九韶於1247年在他所著《數書九章》一書中給出的，有不少書稱為霍納-魯菲尼方法，實際上魯菲尼(P.Ruffini)在1804年，霍納(W.G.Horner)在1819年才分別提出這一方法。

基本介紹

• 中文名：秦九韶方法
• 外文名：Qin Jiushao method
• 所屬學科：數學
• 別名：霍納法則，霍納-魯菲尼方法
• 簡介：求實係數多項式實根近似值的方法

基本介紹

秦九韶方法亦稱霍納法則，是計算多項式值的簡便方法。設多項式

f(x)=a₀x+…+a_n-1x+a_n，

為計算f(x₀)的值可令

f(x)=p(x)(x-x₀)+f(x₀)，

其中

p(x)=b₀x+…+b_n-2x+b_n-1.

比較上式兩邊x的同次冪係數，則得

b₀=a₀，

b_i=a_i+x₀b_i-1(i=1，2，…，n)，

f(x₀)=b_n，

這就是秦九韶方法，計算一個n次多項式的值只用n個乘法和n個加法運算，它也可表示為

f(x₀)=(…((a₀x₀+a₁)x₀+a₂)x₀+…+a_n-1)x₀+a_n，

這種算法計算量少，程式簡單，並且若對p(x)再用同樣算法令

c₀=b₀，c_i=b_i+x₀c_i-1(i=1，2，…，n-1)，

則得f′(x₀)=c_n-1。

相關介紹

類似上面敘述的，可求出各階導數值。秦九韶於1247年在《數書九章》中，第一次用上述方法計算高次方程的函式值，並通過逐次變換與累試，使最後某個累試值x_k，計算出的b_n=f(x_k)=0為止。秦九韶給出的例題都是求正實根，為說明他的求根方法，用現代數學記號並以n=3為例加以說明，設

f(x)=a₀x+a₁x+a₂x+a₃，

若x₀為一近似根，用x-x₀除，相當於在x₀處作泰勒展開

秦九韶的計算公式用表格表示如下：

這裡計算規則是：

本數=上數+(左數×x₀)

而f(x)在x₀的泰勒展開式就是

f(x)=d₀(x-x₀)+d₁(x-x₀)+c₂(x-x₀)+b₃.

例如，求x-67x+1494x-11086=0的根。先估出近似x₀=20。

令y=x-20，方程變為f₁(y)=y-7y+14y-6，估計y₀=3，計算

因b₃=0，故f₁(y)=0的根為y*=3，代入x*=y*+20=23，即f(x)=0的根為x*=23，這就是秦九韶法的計算步驟，但秦九韶法通常是指他的計算高次多項式的算法，它比霍納(W.G.Horner)於1819年提出的同一算法早570多年。