重力測量按其複雜程度,可依次分為標量重力測量、矢量重力測量和梯度重力測量。標量重力測量僅測量重力擾動的大小,而矢量重力測量則能測定整個重力擾動矢量,即擾動引力的三個分量。與標量重力測量相比,矢量重力測量具有其明顯的優勢,它不僅能測出重力異常而且能測出垂線偏差。
基本介紹
- 中文名:矢量重力測量
- 外文名:vector gravimetry
- 類別:測量方法
- 內容:測定重力的大小和方向
基本概念
研究背景
數學模型



測量方法
SINS直接求差估計擾動重力矢量

基於垂線偏差測量的矢量重力估計方法
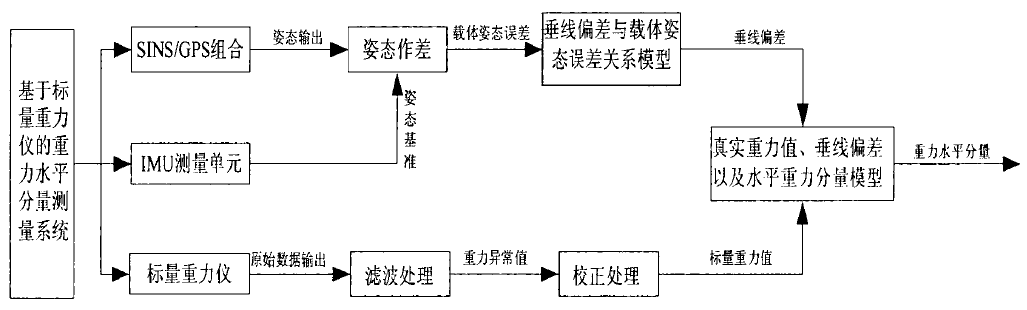
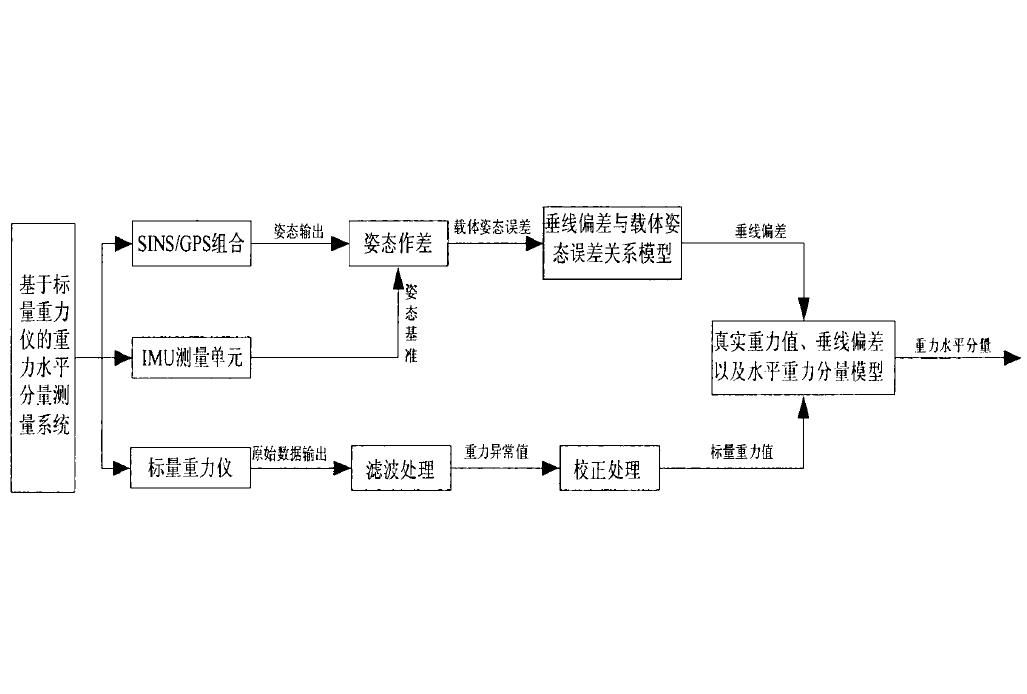
重力測量按其複雜程度,可依次分為標量重力測量、矢量重力測量和梯度重力測量。標量重力測量僅測量重力擾動的大小,而矢量重力測量則能測定整個重力擾動矢量,即擾動引力的三個分量。與標量重力測量相比,矢量重力測量具有其明顯的優勢,它不僅能測出重力異常而且能測出垂線偏差。





重力測量按其複雜程度,可依次分為標量重力測量、矢量重力測量和梯度重力測量。標量重力測量僅測量重力擾動的大小,而矢量重力測量則能測定整個重力擾動矢量,即擾動引力的三個分量。與標量重力測量相比,矢量重力測量具有其明顯的優勢,...
《動態矢量重力測量方法及數據處理關鍵技術的實驗研究》是依託中國科學院精密測量科學與技術創新研究院,由王勇擔任項目負責人的面上項目。項目摘要 SINS/GPS組合系統是進行動態矢量重力測量的一種有效技術途徑。目前國際上正在對該技術開展試驗和研究。SINS/GPS組合系統安裝在運動平台如飛機或汽車上,便可進行航空或陸地...
《矢量重力測量慣性感測器誤差的估計與補償方法研究》是依託中國科學院精密測量科學與技術創新研究院,由柴華擔任項目負責人的青年科學基金項目。項目摘要 矢量重力測量中一個重要的觀測量是比力,它是由捷聯式慣性測量系統中的加速度計和陀螺的觀測給出的。由於加速度存在零偏,陀螺存在漂移,比力觀測將受誤差影響。因此...
《基於SINS/GPS的航空矢量重力測量數據處理方法》是依託武漢大學,由寧津生擔任項目負責人的面上項目。項目摘要 航空矢量重力測量是高效測定中高頻地球重力場信息的先進技術,與地面重力測量、海洋重力測量和衛星重力測量技術相互補充,在資源勘探、大地測量、地球物理及國防建設等領域具有重要的科學意義和廣泛的套用價值。為...
航空矢量重力測量同時確定重力異常矢量的大小和方向,分為平台式和捷聯式,其原理與標量類似。航空梯度重力測量是利用同一穩定平台上的兩組三軸加速度計測定異常位的二階梯度,因此空中定向由穩定平台維持。發展現狀 航空重力測量技術的發展是伴隨著其三個主要組成部分的發展而發展的。在1990年以前,由於受限於所用設備...
《捷聯式航空重力矢量測量誤差分離技術研究》是依託中國人民解放軍國防科技大學,由張開東擔任項目負責人的面上項目。中文摘要 航空重力測量作為一種動態快速測量方法是近二十年來重力測量的研究熱點之一,捷聯式航空重力儀具有體積小、重量輕、功耗小等優勢,代表了航空重力儀的發展方向,而矢量測量更是航空重力測量的遠期...
第2章航空重力矢量測量理論基礎23 2.1航空重力測量基本原理23 2.2慣性器件的誤差模型24 2.2.1加速度計的誤差模型24 2.2.2陀螺的誤差模型25 2.3SINS/GNSS重力矢量測量方法25 2.3.1基本原理26 2.3.2重力矢量測量的數學模型和誤差模型33 2.4航空重力矢量測量的誤差分析34 ...
在新定義下以地面為非慣性系,利用力的平衡原理可以較嚴密地推導出地面上物體所受重力的矢量表達式。(統一用F代表萬有引力,f代表慣性力,G代表重力,N代表支力。黑體字母代表的是矢量,下面進行的是矢量運算)放在支持物上的物體受到地球的萬有引力F,還有太陽的萬有引力F,月球的萬有引力F,及其他星球的萬有...
這個加速度稱為自由落體加速度,是由物體所受的重力產生的,也稱為重力加速度,通常用字母g來表示。重力加速度是矢量,它的方向總是豎直向下的,它的大小可以用實驗方法求出。實驗證明:重力加速度的大小隨其在地球上地點的不同而略有差異。例如在赤道上g=9.780 m/s²,在北極g=9.832 m/s²,在北緯45...
質量的單位是千克(kg),重力的單位是牛頓(N).是否矢量 質量僅有大小,沒有方向;重力不但有大小,而且有方向,且方向總是豎直向下.大小與地理位置 同一物體在任何位置質量大小均不變,物體的重力大小會隨地理位置的變化而變化.計算公式 m=ρV, G=mg(g約等於9.8,因所在地的海拔不同而有所差異,一般是海拔越高g...
因此,準確記錄扭力系統的偏角,就可以求出重力位的二次導數。由於扭力系統的靈敏度很高,秤臂穩定下來的時間較長。同時還需要在3~5個方向上照相記錄,所以,儀器附有自動控制系統,並安放在特製的小房裡工作。儀器的操作和測量結果的計算都比較煩瑣,每測—個點需要2~3小時,工件效率較低。扭秤的測量結果用矢量...
。這種重力梯度儀以微小的體積和重量( 小於1 kg) ,或許會成為未來衛星重力梯度測量儀器的一個發展方向。其基本結構如圖 3所示。靜電懸浮 靜電懸浮加速度計重力梯度儀就是將基於靜電懸浮原理製成的加速度計放置在不同的矢量方向,通過差分原理測量該矢量方向上重力梯度張量。由於靜電懸浮加速度計利用靜電力平衡檢驗質量...
研究地球重力場的一種數學方法。地球外部重力場的延拓,主要是指由地面觀測數據計算空間某一高度的重力矢量,或由空間觀測數據計算地面上的重力矢量。前者稱為向上延拓,套用於改正空間飛行器軌道的擾動,提高慣性導航系統的精度;後者稱為向下延拓,套用於航空重力測量和衛星重力梯度測量值的歸算。 [1] ...
重力敏感器 重力敏感器提供的重力數據可用於無源導航和地形測量。重力敏感器包括重力梯度儀和重力儀,重力儀測量重力異常或重力矢量的大小相對標準地球模型的偏差。重力梯度儀測量重力梯度即重力在三維上的變化率。重力敏感系統(GSS)最初是為了補償垂線偏差用的。最近成功地用於無源導航和地形測量中。80年代中期用的GSS為...
4.2 基於重力矢量測量的加速度計零偏估計算法 4.2.1 加速度計零偏估計算法設計 4.2.2 捷聯式重力矢量測量噪聲模型 4.2.3 重力矢量測量噪聲模型參數 4.2.4 加速度計零偏估計算法 4.3 加速度計零偏估計算法仿真驗證 4.3.1 重力數據仿真 4.3.2 加速度計零偏參數設定 4.3.3 零偏估計算法...
實際套用中,一般將複雜的地球重力場解析化,並基於擾動位的泛函,可以十分方便地表示和提供大地水準面、重力異常、垂線偏差、擾動重力等擾動位的派生物。這種理論和實際套用上的優勢,使得地球重力場模型在大地測量學、地球物理學、地球動力學、地質學、海洋學、生物學、空間和軍事等學科和領域具有十分廣闊的套用前景。...
4.1基於磁場/重力在固定坐標系投影不變原理校正法 4.1.1校正原理 4.1.2固定坐標系投影不變原理校正法實驗分析 4.2基於磁場/重力在平面垂向投影不變原理校正法 4.2.1校正原理 4.2.2平面垂向投影不變原理校正法實驗分析 4.3兩種非對準校正法效果對比 4.4重力擾動分析 4.4.1重力擾動引入的慣導測量誤差 ...
2.7 矢量和張量 2.8 能量動量張量 2.9 粒子的自旋 第3章 廣義相對論基礎 3.1 等效原理 3.1.1 引力質量與慣性質量 3.1.2 等效原理的精確表述 3.1.3 度規張量與粒子在引力場中的運動 3.1.4 運動方程的牛頓極限 3.1.5 引力頻移效應 3.1.6 廣義協變原理 3.2 近代數學物理幾何方法 3...
。因此,我們常說Cavendish是歷史上第一個“稱量”了地球質量的人,他也因此成為歷史上第一個測量萬有引力常數G的科學家。繼Cavendish之後,具有代表性的測G工作當屬1895年Boys的實驗,其原理與Cavendish扭秤方法完全相同。直到1942年,他們的結果才被Heyl採用扭秤周期法測量的結果所取代[25,26]。Heyl提出的採用扭秤...
.(3)捷聯式航空重力儀動態誤差的分離。主要是基於相關分析的動態誤差分離,對動態誤差抑制過程的殘留誤差進行分離。結題摘要 基於捷聯慣導的航空重力儀具有體積小、重量輕、功耗小、成本低、可靠性高等優點,並且可以實現無人操作和矢量測量,是航空重力儀的一個重要發展方向。但是基於捷聯慣導的航空重力儀目前國內外還...
認為強震前重力等位面的彎曲程度異常變化,要大於重力等位面上的傾斜異常變化。這一認識從王貴宣等在研究唐山地震前的西集台重力位2次偏微商的變化中也得到證實,即唐山地震前觀測到異常期間,除梯度矢量G值變化很小外,曲率值R(K)有明顯變化。
對重量的解釋有許多說法,例如,重量就是重力;物體的重量就是地球對該物體的萬有引力;重量即物體所受重力的大小;重量是物體靜止時,拉緊豎直懸繩的力或壓在水平支持物上的力。上述幾種講法,有的強調重量即重力,是矢量,它們的本質是引力。有的強調重力不是矢量,重量是重力的大小,是標量。還有的是以測量...
物重(quality)是指一個物體受到重力的大小。是力所以是有向的量,矢量,方向豎直向下。聯繫和區別 聯繫 物體的物重和它的質量成正比。即G=mg g=9.8N/kg 區別 質量是物體中含有物質的多少。是物體的一種屬性。而物重是由於地球對物體的吸引而使物體受到的力。質量是沒有方向的量,即標量。物重是力所以是...
上述幾種講法,有的強調重量即重力,是矢量,本質是引力。有的強調重力不是矢量,重量是重力的大小,是標量。還有的是以測量法則作為重量的定義。這些不同的定義只是解釋的不同而已,談不到對與錯。計算公式 質量與重量換算公式:,其中G為重量,m為質量,g為自由落體加速度,於地球表面約為9.8m/s²。單位 質...
用單擺測重力加速度是單擺周期公式 的一個重要套用。 [1] 動力學方程 播報 由牛頓力學,單擺的運動可作如下描述。 首先可以得到,重力對單擺的力矩為 其中m為質量,g是重力加速度,l是擺長,θ是單擺與豎直方向的夾角,注意,θ是矢量,這裡取它在正方向上的投影。 希望得到擺角θ的關於時間的函式,來描述單擺運動。
儀器的操作和測量結果的計算都比較煩瑣,每測—個點需要2——3小時,工件效率較低。測量結果 扭秤的測量結果用矢量圖表示,用一短線表示曲率,矢量方向相應於最小曲率平面的方位,矢量長度表示等位面曲率差大小 。在短線中心以箭頭畫出總梯度,指向重力增加的方向。扭秤的靈敏度很高並可測多個參數,但是也有其不足之...
協調加速度計可用於測量在空間分離中適當加速度,特別是重力的差異;即重力場的梯度。這種重力梯度是有用的,因為絕對重力是一個很弱的影響,取決於地球的局部密度是非常可變的。加速度計的單軸和多軸型號可用於檢測正確加速度的大小和方向作為矢量,並可用於檢測取向(由於重量變化的方向),坐標加速度,振動,衝擊和...
′是測點在局部坐標系中的位置矢量;m是尺度改正數;R是一個旋轉矩陣,它的元素是獨立的歐拉角εx、εy、εz,表示圍繞局部坐標系x、y、z軸的旋轉。計算這些轉換參數至少要有3個公共點,它們在兩種坐標系中的位置都是已知的。由此法所得地心坐標轉換參數的精度可達1~3米。建立地心坐標系的第一類經典重力測量...
協調加速度計可用於測量在空間分離中適當加速度,特別是重力的差異;即重力場的梯度。這種重力梯度是有用的,因為絕對重力是一個很弱的影響,取決於地球的局部密度是非常可變的。加速度計的單軸和多軸型號可用於檢測正確加速度的大小和方向作為矢量,並可用於檢測取向(由於重量變化的方向),坐標加速度,振動,衝擊和...
高精度慣性導航基礎.北京:國防工業出版社,2002.套用 在一般線加速度計中測量的是比力(a+g)不能分辨出重力加速度g和運動加速度a 一個加速度計只能測量一個方向的比力,測量矢量必須使用三個加速度計;測量值與安裝方向、姿態有關,且受安裝精度影響。三個加速度計垂直安裝可測量比力矢量,進而得到運動加速度。
