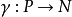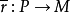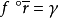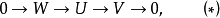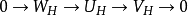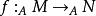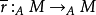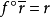相對投射模(relatively projective module)是比投射模性質稍弱的一類模,山度米爾斯基(Sandomierski)於1964年將投射模和內射模推廣到相對投射模和相對內射模。
基本介紹
- 中文名:相對投射模
- 外文名:relatively projective module
- 所屬學科:數學
- 所屬問題:模論
- 相關人物:山度米爾斯基(Sandomierski)
- 相關概念:投射模,擬投射模等
基本介紹,相關概念,內射模,投射模,擬投射模,
基本介紹
設R是一個交換環,G是一個有限群,H是G的子群,V是一個有限生成的RG模,若對於每個RG模的正合列
1. V是H投射的。
2. V是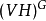 的直和項。
的直和項。
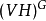
3. 存在一個有限生成的RH模W,使V是 的直和項。
的直和項。

4. 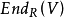 是H投射的RG模。
是H投射的RG模。
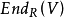
5. 存在 使
使

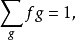
相關概念
內射模
內射模(injective module)是投射模的對偶概念,設Q是左A模,若函子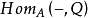 正合,則稱模Q為內射模;這等價於:對每個單同態
正合,則稱模Q為內射模;這等價於:對每個單同態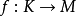 ,及每個同態
,及每個同態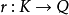 ,一定有同態
,一定有同態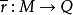 ,使得
,使得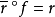 成立,對任意模M,一定存在內射模E,使得M是E的子模。若E是左A內射模,且E是左A模M的子模,則E是M的直和因子。若A是環,則存在充分多的左A內射模,例如,若Q是可除阿貝爾群,則
成立,對任意模M,一定存在內射模E,使得M是E的子模。若E是左A內射模,且E是左A模M的子模,則E是M的直和因子。若A是環,則存在充分多的左A內射模,例如,若Q是可除阿貝爾群,則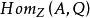 是A內射模。貝爾準則是一個很有用的判別定理:對A的每個左理想I和每個A同態
是A內射模。貝爾準則是一個很有用的判別定理:對A的每個左理想I和每個A同態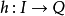 ,若h都可開拓成
,若h都可開拓成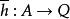 ,即
,即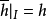 ,則Q是內射模;反之亦然。內射模這一概念是由貝爾(R.Baer)於1940年提出的;詹森(R.E.Johnson)和黃德華於1961年將投射模、內射模這些概念推廣到擬投射模和擬內射模;山度米爾斯基(Sandomierski)於1964年推廣到相對投射模和相對內射模。
,則Q是內射模;反之亦然。內射模這一概念是由貝爾(R.Baer)於1940年提出的;詹森(R.E.Johnson)和黃德華於1961年將投射模、內射模這些概念推廣到擬投射模和擬內射模;山度米爾斯基(Sandomierski)於1964年推廣到相對投射模和相對內射模。
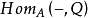
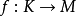
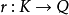
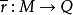
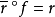
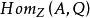
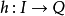
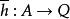
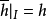
投射模
投射模(projective module)是比自由模更一般的模,它是內射模的對偶概念。設P是左A模,若有左A模Q使P⊕Q同構於自由A模,則P稱為投射A模。這等價於:函子HomA(P,-)是正合的;也等價於:對每個滿同態 ,及每個同態
,及每個同態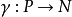 ,一定有同態
,一定有同態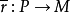 ,使得
,使得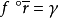 成立,對右A模有類似的定義與性質。任意左A模M必是某一左A投射模的商模;環A作為A模當然是投射模,自由模一定是投射模,投射模一定是平坦模;反之都不一定成立,當環A是主理想整環時,每個投射模都是自由模,塞爾(J.P.Serre)於1955年曾提出一個著名的猜測(塞爾猜測):域F上的多項式環
成立,對右A模有類似的定義與性質。任意左A模M必是某一左A投射模的商模;環A作為A模當然是投射模,自由模一定是投射模,投射模一定是平坦模;反之都不一定成立,當環A是主理想整環時,每個投射模都是自由模,塞爾(J.P.Serre)於1955年曾提出一個著名的猜測(塞爾猜測):域F上的多項式環 上的每個有限生成的投射模是否是自由模?奎倫(D.G.Quillen)和蘇斯林(М.Я.Суслин)幾乎同時於1976年用不同方法給以解決(他們得出更強的結果,即只要限制F為主理想整環即可)。另外,交換諾特局部環上每個有限生成的投射模也是自由的,這個結果首先由卡普蘭斯基(I.Kaplansky)於1958年得到,投射模在模論、同調代數、代數K理論中有重要套用。
上的每個有限生成的投射模是否是自由模?奎倫(D.G.Quillen)和蘇斯林(М.Я.Суслин)幾乎同時於1976年用不同方法給以解決(他們得出更強的結果,即只要限制F為主理想整環即可)。另外,交換諾特局部環上每個有限生成的投射模也是自由的,這個結果首先由卡普蘭斯基(I.Kaplansky)於1958年得到,投射模在模論、同調代數、代數K理論中有重要套用。