相和相變

一個處於熱力學平衡狀態的物質系統，可以是一個各處物理和化學性質都相同的均勻系；也可以由若干個有邊界可分的均勻的部分組成，各部分之間的性質存在著差別；每一個均勻的部分叫做一個相。前類系統稱為單相系；後類系統稱為復相系。不同相之間發生的轉變稱為相變。

基本介紹

• 中文名：相和相變
• 外文名：Phase and phase transitions
• 性質：物質系統
• 特點：處於熱力學平衡狀態

相和相變

一個處於熱力學平衡狀態的物質系統，可以是一個各處物理和化學性質都相同的均勻系；也可以由若干個有邊界可分的均勻的部分組成，各部分之間的性質存在著差別；每一個均勻的部分叫做一個相。前類系統稱為單相系；後類系統稱為復相系。
物質的氣態只有一種結構，多種氣體互相混合，也只能形成一個均勻的單相。物質的液態一般只有一個相；液態氦則有兩個相，分別稱為氦Ⅰ和氦Ⅱ。兩種不同的液體若能混合，則形成一個均勻相；若不能混合，如水和油，就會出現分界面，形成兩相。物質的固態情況較複雜，結晶態可以有多種結構，它們分別屬於不同的相。例如水在高壓下有六種不同的結晶態，分別屬於六種不同的相；又如硫的固態有單斜晶系和正交晶系兩種結構，即兩種相。而非晶態只有一個相。不同相之間發生的轉變稱為相變。如在低於臨界壓強下，氣體的溫度降到某一數值時就液化；在一定的壓強下，把固體加熱到某一溫度時，發生熔解；鐵磁性物質的溫度上升到居里點以上時，其鐵磁性就過渡到順磁性；這些都是相變現象。　相變理論　相平衡曲線和克拉珀龍方程　穩定在一定溫度和壓強下的物質的單相系，當溫度和壓強改變到某一範圍內時，其穩定性遭到破壞，系統只有改變自己的結構才能得到新的穩定，這時出現兩相或多相共存的穩定狀態。對於單元系(只含一種化學組分的物質系統)兩相共存的條件是:兩相的溫度T、壓強p以及化學勢μ都必須相等。根據

μ1(T,p)=μ2(T,p) (1)

這個條件，給出了兩相共存時的壓強對溫度的依賴關係

p=p(T)。 (2)

此式所描繪的曲線稱為相平衡曲線。以p、T為直角坐標，描繪出相平衡曲線，曲線上的點表示兩相共存狀態，曲線兩側的區域是單相區，這個圖形叫相圖。
同一種物質的三相平衡應由式

μ1(T,p)=μ2(T,p)=μ3(T,p) (3)

確定，式中T、p代表三個相的共同溫度和共同壓強，三相共存的狀態在相圖上由孤立的點來表示，這個點稱為三相點，它就是三條相平衡曲線的交點。熱力學理論指出,對單元系來說,可以共存的相的數目不可能多於3(見吉布斯相律)。圖1表示水的相圖，Pt代表三相點。在適當的溫度和壓強範圍，任何物質都有三相點。如果在相變過程中,伴隨有一定熱量的放出或吸收,則稱這一熱量為相變潛熱。相圖中的曲線都由實驗測定，套用熱力學理論則可求出曲線的斜率同潛熱之間的關係為

， (4)

式中λ是1摩爾物質由2相變到1相的相變潛熱，s1、s2、v1、v2分別是1相和2相的摩爾熵和摩爾體積。它描述了氣-液相、液-固相和固－氣相間的轉變。此式是E.克拉珀龍於1834年得到的，由於R.克勞修斯套用熱力學理論也導出了這個方程式，故又稱克拉珀龍－克勞修斯方程,它表示當溫度變化時，處於平衡的兩相壓強的變化。當溫度和壓強變到某個值，氣液之間不再出現兩相共存區,而是連續地過渡,則這點稱為臨界點(見圖1中的c點)。例如水的臨界點是Tc=374.15℃,pc=261.5標準大氣壓。臨界點隨不同的物質而異。可由下面方程決定

，
。 (5)

同時，臨界態本身應當是穩定的，按熱力學理論穩定性條件應是

。 (6)

應當注意的是，滿足穩定性條件的區域中，還有一部分屬於亞穩狀態，它們是過冷相或過熱相。　相變的級 　通常的相變發生在一定的壓強和溫度下，又稱為一級相變。其特點是：兩相的化學勢相等，但化學勢的一級偏導數所代表的性質發生突變，即摩爾熵和摩爾體積發生突變，但其改變為一有限量，有相變潛熱。實驗上還發現了另一類相變，稱為二級相變。其特點是：兩相的化學勢和化學勢的一級偏導數均相等；化學勢的二級偏導數所代表的性質發生突變，且改變一有限量。也就是說，這類相變既無潛熱，也無體積變化，但比熱容、定壓膨脹係數、等溫壓縮係數發生突變。三級相變的特點是：兩相的化學勢和化學勢的一級、二級偏導數均相等,化學勢的三級偏導數發生突變。M.von勞厄曾提出兩種液態氦之間的相變屬於第三級相變，可是未得到公認。倘若某種相變具有如下的特點：兩相的化學勢和化學勢的一級、二級直至(n-1)級偏導數全相等，而n級偏導數發生突變，且改變數是有限的,這種相變稱為n級相變。
厄任費斯脫二級相變方程 　P.厄任費斯脫在研究氦Ⅰ和氦Ⅱ之間的相變時，導出二級相變的厄任費斯脫方程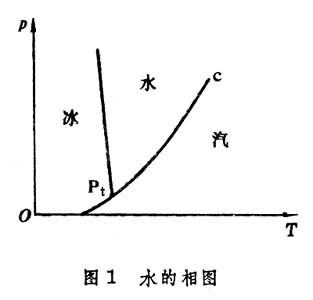

， (7)

， (8)

式中 сp、α、κ分別是定壓比熱容、定壓膨脹係數和等溫壓縮係數。　上述討論可推廣到其他物性，例如存在外磁場時超導態和正常態之間的相變情形。某些金屬和合金在低於一定的轉變溫度（即臨界溫度）Tc時，電阻突然變為零，此時這些金屬變為超導體，譬如鈮的轉變溫度Tc為8.7K，錫為3.7K，在Tc之下，超導態也可以在一定的磁場值Hc下消失，轉入正常態。實驗給出Hc和溫度T(T<Tc)的曲線為

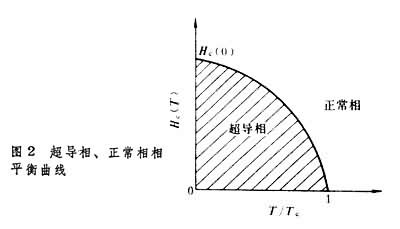
， (9)

式中Hc(0)是當T→0K時Hc(T)的值。圖2曲線兩側分別為超導相和正常相，故此曲線亦屬相平衡曲線。按照熱力學理論，超導相和正常相平衡時，它們的單位體積熱力勢g相等。

gs(T,Hc)=gn(T,Hc)。 (10)

從此式出發，即可得到以下形式的相平衡曲線方程式

， (11)

式中ss、ms分別是超導相的單位體積熵和磁化強度,sn、mn是對應正常相的量。其實只要把式(4)中的(p,υ)換成(-Hc,m)就行了。由於超導體又是一理想的抗磁體,故內部的磁感應強度等於零，則有

As=H+4πms=0。 (12)

而正常導體的磁導率μ一般約等於1,故mn=0,由式(11)和(12)即得

。 (13)

由圖2看出，，因此sn>ss。只有在T=Tc處,兩相的單位體積熵相等。所以，可得出如下結論：
①當T<Tc時,因外場存在而發生的相變有潛熱,為一級相變；
②當T=Tc時的相變無潛熱，屬二級相變（忽略體積變化）。
方程式(7)、(8)可用於cP、α、κ等量在突變點為有限的情形。除超導態和正常態在零磁場下的轉變屬於這類相變外，鐵磁和順磁相變，合金的有序和無序相變以及 HeⅠ-HeⅡ轉變由於熱容在相變點都是發散的，故都不適用，而把這類在突變點處熱容呈現發散的二級相變稱為λ相變。圖3給出關於氦的實驗相圖，其中λ點是T=2.19K，p=0.058標準大氣壓。　朗道二級相變理論Л.Д.朗道從相變點處的對稱性質的變化研究相變點領域的行為，他採用一個序參量η來描述相變，η=0代表一種序比較低即對稱性比較高的結晶狀態，即無序態；η厵0則代表一種序比較高即對稱性比較低的結晶狀態， 即有序態。η是有序程度的量度，可由它所取的兩種不同的值：或零，或有限值區分系統處於哪一相，而系統的熱力學性質譬如熱力勢同η有關。在一定的溫度T和壓強p之下，η的平衡值ηe同T、p有關，它由熱力勢的極小條件

(14)

決定，由此式解出η=ηe(T,p)，當T，p連續變到相變點時，ηe也連續地變為零。所有的相變點應是每個相的穩定性開始遭到破壞，或者穩定性條件

(15)

開始不適用的點，它處於穩定區和不穩定區的邊界區域。對於二級相變來說,由於無共存區,因此，相變點是滿足

ηe(T,p)=0 (16)

的臨界態。由此式可畫出相平衡曲線。
例如，鐵磁體在居里溫度以下，存在自發磁化，這屬於在方向上對稱性比較低的狀態；當溫度升高時，有序程度降低,自發磁化變小；當溫度達到居里溫度時,自發磁化等於零，此時系統處於對稱性較高的狀態，稱為順磁狀態。於是可以把自發磁化作為序參量，它是一個矢量，記作ηi(i=1,2,3)。ηi=0代表順磁態，ηi厵0代表鐵磁態，ηi同T、p有關，其值由磁介質系統的熱力勢G(T，p，η)極小條件確定。關於超導相和正常相的相變問題，也可套用這種方法。朗道二級相變理論得出的結論是正確的，並且有相當的普遍性。
相變模型及其統計物理學解釋　相變是極其普遍的現象，為了正確地闡明發生相變的機理，需要套用統計物理學理論。它對處於平衡態的系統給出了求配分函式的方法，但要具體求解，必須有相應的模型和手段。統計物理學關於相變問題的理論研究只能套用於一些簡單的模型。
例如，非理想氣體凝聚為液體時，物態方程要出現某種不連續性。圖4表示在非理想氣體的等溫線上，對應於同一個pc，比容v=v(p)發生了一個突變。υ由氣相比容υg變到液相比容υ1。　套用統計物理學理論可以得到如下結論：對於有限體積，系統沒有異常行為,p-υ圖上不可能發生凝聚現象，只有當體積V→∞時,才可得到由巨配分函式Ξ 所表示的熱力學極限：

，

(17)

因而有可能發生如圖4所示的相變，式中ρ為密度，，是熱波長。李政道和楊振寧於1952年提出兩條定理，論證了相變發生的可能性和條件。
為了能在平衡態統計物理的範圍內研究固體中的某些相變，人們提出了各種模型。
鐵磁性模型 　當溫度在居里溫度以上時，鐵(Fe)鎳(Ni)這類金屬中，原子自旋的取向是無規的，不產生淨的磁矩；當溫度低於居里溫度時，原子的自旋自發地擇優取向，結果在此方向發生自發磁化。當溫度從高溫一側趨向居里溫度時，比熱容趨向無窮大，這是一種從非鐵磁性狀態到鐵磁性狀態的相變。鐵磁性模型就是研究這類相變的一類簡單的模型。
假設在周期性點陣的每個陣點上有一個自旋si(i=1,2,…),只考慮最近鄰自旋之間的相互作用和每個自旋同外磁場的相互作用，則這個系統的哈密頓量應為

， (18)

式中是對最近鄰自旋對求和，H是加在z方向上的外磁場強度，μ0是每個自旋的磁矩，是第i個自旋算符的z方向分量，Jij是最近鄰自旋對〈i，j〉的相互作用能或稱交換積分，它僅同自旋間的距離有關，對於鐵磁性物質Jij>0,對於反鐵磁性物質Jij<0。具有這樣的哈密頓量的鐵磁性模型稱為海森伯模型,若z方向分量對哈密頓量的貢獻很小,可以略去,又x及y方向屬各向異性，於是式(18)變為式中ξij是決定於自旋i和j之間距離的常數,這個模型稱為XY模型。若磁各向異性是z方向分量對哈密頓量的貢獻占絕對優勢，而x、y方向分量的貢獻可以忽略時，則式(18)變為

， (20)

式中取值+1/2或－1/2。這時，不考慮式(18)的哈密頓量所具有的算符對易性這個量子力學效應。這種模型就是在相變理論中占有重要地位的伊辛模型。略去上標z，並取s=±1,，就得到伊辛模型哈密頓量常用的表示

， (21)

式中ε為最近鄰自旋對相互作用能量。對於鐵磁物質ε0。
點陣氣體模型 　是一種非真實氣體模型，按照這個模型，N個可分辨的粒子排列在周期點陣的N0個陣點上，每個陣點最多只能為一個粒子占據，每個粒子僅同其最近鄰的粒子發生作用。
圖5是二維點陣氣體模型的示意圖，圖中“。”代表空位，“·”代表陣點上有粒子占據。這種模型是為了便於將伊辛模型所研究的鐵磁性相變同一般的氣－液相變進行比較並作統一考慮而提出的。這N個粒子系統的總能量為

， (22)

式(22)中uij是i、j陣點上的兩個粒子的相互作用能,如以rij表示粒子i和粒子j的距離，則

(23)

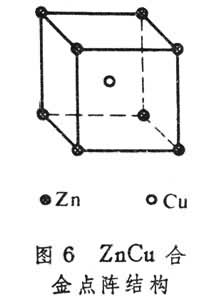
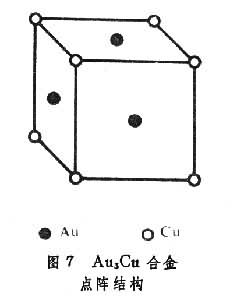
　有序－無序相變 　這是一個實際問題。如體心立方結構的鋅銅合金（ZnCu合金），面心立方結構的金三銅合金（Au3Cu合金）,它們的點陣分別由兩套簡單立方格子和四套簡單立方格子構成,如圖6和圖7所示。實驗證明:當溫度T→Tc（相變溫度）時,比熱容c→∞。當TTc時,就完全被破壞。每個陣點對於各種原子來說都是等價的，因而占位是無規的。這種相變稱為有序－無序相變。認為處於陣點上的粒子僅同其最近鄰陣點上的粒子之間存在著相互作用。以N和N和N分別代表最近鄰為 AA、BB和 AB的最近鄰對總數,NA、NB和N0分別表示A原子總數、B原子總數和總陣點數,ε、ε和ε分別表示最近鄰對AA、BB和AB的相互作用能。則有序-無序相變系統的相互作用總能量為

。 (24)

　伊辛模型、點陣氣體模型和有序－無序相變問題中的UI、Ug和U0-d經過簡單的運算以後可以寫成相似的形式，所以在計算它們的配分函式或諸熱力學量時也可用統一的方法處理。對伊辛模型的計算結果，也可以用到其他兩個問題上。
方法　20世紀30、40年代以來，許多科學家對上述的幾種相變模型求解，採用的方法主要有平均場近似、高溫展開和低溫展開、解析法、數值法以及重正化群方法等。
平均場近似 　它是處理伊辛模型的一種近似方法。對於三維的真實情形，須作某種近似，即P.外斯的平均場理論。考慮把每個陣點的自旋si都用由下式

(25)

定義的一個序參量η來代替。顯然，當時，全部自旋的磁矩都同磁場平行，磁極化達到了飽和，此時η=1；當時，整個系統磁化為零,η=0。可見η是描述系統極化狀態的參量。用獨立的自旋在等效的外磁場H┡中的勢能代替各對自旋的相互作用能。任何一個自旋（不管向上或向下）所受到的最近鄰自旋的作用均等於H┡,在一定的溫度下和的平均值是一定的，因此,具有一定的值。可以得到自洽方程

。 (26)

不存在外磁場(H=0)時上式變為

。 (27)

用圖解法求出在ε<0（鐵磁性物質）情形下的解

(28)

式中Tc是居里溫度

， (29)

η0是式(27)的大於零的根。在T=0和T=Tc附近，得到近似值

，

， (30)

是磁化強度。還可以求出能量、熵、亥姆霍茲自由能（見自由能）等各個熱力學量,當T>Tc時,它們都等於零,當T<Tc時,它們都是η0的偶函式。這表明存在由式(29)給出的臨界溫度Tc,在Tc以上,當H=0時,物質不磁化；在Tc以下,儘管H=0，但磁化強度不為零,它可正可負，且無論磁化強度是正還是負，熱力學函式均相同，故在臨界溫度以下，鐵磁性物質存在相變。
20世紀40年代L.昂薩格對一維、二維伊辛模型採用解析法,獲得了不存在外磁場條件下的嚴格解,表明：一維伊辛模型不存在相變，二維的在一定條件下發生相變。這種方法具有指導性的意義。
臨界指數和標度假定 　是凝聚和相變問題的一個重要方面，它作為研究物質的相變現象和臨界性質的一種有效手段，近20年來有了很大的發展。
由實驗知道，各種物質發生相變時，隨著溫度趨近臨界溫度Tc，物理量一般以的規律變化，μ是描述相轉變的指數，稱為臨界指數。
圖8中虛線表示氣、液兩相共存曲線,在它之下為二相區。當T<Tc（臨界溫度）時,液體密度ρ1同氣體密度ρg差別很大，但達到Tc時,ρ1同ρg的差別趨於消失。這個特徵表示存在一個序參量，它在Tc以上取值為零，在Tc以下，取非零的值,在這裡可取序參量為ρ1-ρg，於是有

， (31)

式中β>0稱為臨界指數，由實驗確定。實驗指出，等溫壓縮係數κT和定容比熱容cV，當T=或時,均發散。其實由圖8看出,因而κT→∞，仿照式(31)，也可定義κT和cV的臨界指數，它們分別為－γ，-γ┡和-α，-α┡。　對於磁性系統，序參量取為自發磁化強度，並用下述一般公式定義臨界指數b，即可寫成

， (32)

根據式(32)列表1。表中,，m為磁化強度，r為分子間距離,d為系統維數。表1共列出9個臨界指數:-α、-α┡、β、-γ、－γ┡、δ、-v、-v┡、η。發現鐵磁性和液體兩個系統的臨界指數－α、β、-γ、δ均非常接近。將伊辛模型分別用平均場近似、二維昂薩格嚴格解和計算機數字解計算六個臨界指數得到的數值和各種鐵磁物質相應的臨界指數的實驗值列於下表。 　可見利用各種模型和方法算出的臨界指數雖互不相同，但它們之間的某些關係對於各種模型和方法來說幾乎完全相同，並同實驗的測量結果符合。從此表容易看出，α、α┡、β、γ、γ┡和δ之間滿足以下關係

(33)

此式是聯繫各臨界指數的關係式，稱為標度律。1966年前後，L.P.卡達諾夫從標度假設出發，推出這些關係式。考慮伊辛模型，引入參量，現討論由每邊L個自旋組成的集團,L=2情形如圖9所示，假設標度變換為
tL=tLa，hL=hLb， (34)
並認為在臨界溫度附近，以參量t、h的自旋元胞問題同tL、hL的自旋集團問題等價，即有每個自旋的熱力勢的關係式

g(tL,hL)=Lbg(t,h)。 (35)

注意式(34)中指數a、b不能由標度假設確定。那么運用式(35)及一些熱力學關係式，容易推導出各臨界指數同a、b的關係式，從而得到如下標度律

。 (36)

這樣，標度假設就把9個臨界指數並為兩個獨立指數,因此這個假設是可取的，所得到的標度律非常有用，但對這個假設的解釋尚不清楚。　重正化群法 　1971年K.G.威耳孫推廣量子場論中重正化群方法，把它用於相變和臨界現象中，得到了很好的結果，他也因此獲得1982年諾貝爾物理學獎。
相變理論處理的問題是一個十分複雜的多體問題，必須採用減少自由度的辦法來解決。標度變換體現了重正化群變換的基本思想，不去直接計算配分函式，而是討論那些使配分函式保持不變的變換性質，從而抓住相變的主要特徵。
重正化群變換性質有兩個步驟:①進行粗粒平均,由於當T=Tc時,關聯長度ξ→∞,則元胞自旋可用集團平均值代替、相互作用可用自旋集團間的有效作用代替。若每個集團內有n個自旋，則在坐標空間的平均為

。 (37)

也可在動量空間平均，完成對自旋變數的傅氏變換，

(38)

短波部分的積分。這樣,“尺子變長”,解析度降低，關聯長度（見相關函式）也相應地縮小了。②進行標度變換，使其同原來模型一致。對尺度:，，整個系統收縮s倍；對自旋，這好像用倍數低的顯微鏡觀察，當然就不能看到細節的情況。把①、②兩步合起來的變換用Rs表示，得到哈密頓量的變換式，Rs一般是非線性變換。可以證明

。 (39)

故這個變換形成半群，稱為重正化群。經過以上手續把同其自由度有關係的相互作用重新作了調整，因而減少了自由度。再把Rs變換下的不動點同連續相變聯繫起來分析連續相變下的特徵。

參考書目

龔昌德編：《熱力學與統計物理學》，人民教育出版社，北京1982。
戶田盛和、久保亮五編：《統婖物理學》，岩波，東京，1978。
郝柏林等編著：《統計物理學進展》,科學出版社,北京，1981。