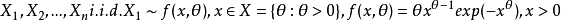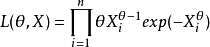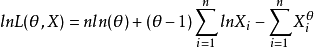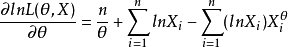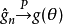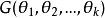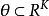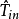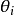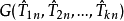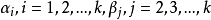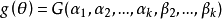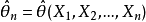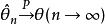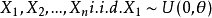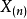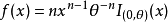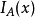相合估計亦稱為一致估計、相容估計,估計量的一種大樣本性質為:當樣本容量n充分大時,估計量可以以任意的精確程度逼近被估計參數的真值。按收斂意義不同,可以區分不同的相合性,常見的有:弱相合估計、強相合估計、r階相合估計,這三種相合性之間的關係與三種收斂性的關係是完全一致的。相合性是一個估計量所應具備的最基本的性質。
基本介紹
- 中文名:相合估計
- 外文名:consistent estimation
- 別名:相容估計,一致估計
- 類別:弱相合估計、強相合估計
- 特點:強相合估計量必為相合估計量
- 套用領域:數理統計
定義
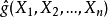
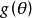
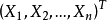
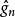
相合估計量
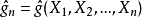
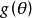
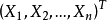
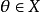
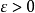
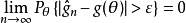
強相合估計量
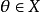
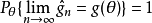
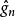
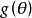
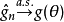
兩者的關係
相關定理
定理1
定理2
定理3
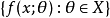
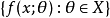
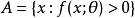
定理4
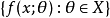
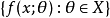
典例
例1
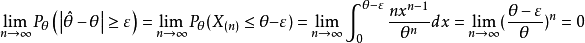
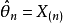
例2