基本介紹
- 中文名:漸近正態估計
- 外文名:asymptotically normal estimate
- 簡稱:CAN估計
- 所屬學科:數學(統計學)
- 別名:相合漸近正態估計
- 舉例:樣本均值,樣本矩等
基本介紹

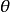
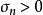
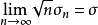
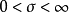
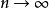
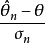

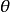
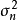


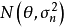


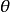
相關概念與定理

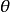
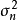
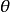
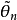
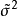
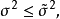

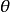

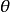
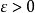
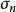

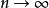
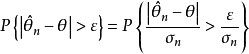
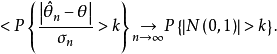
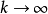
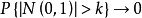
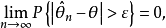

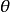
例題解析
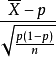
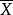
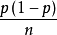
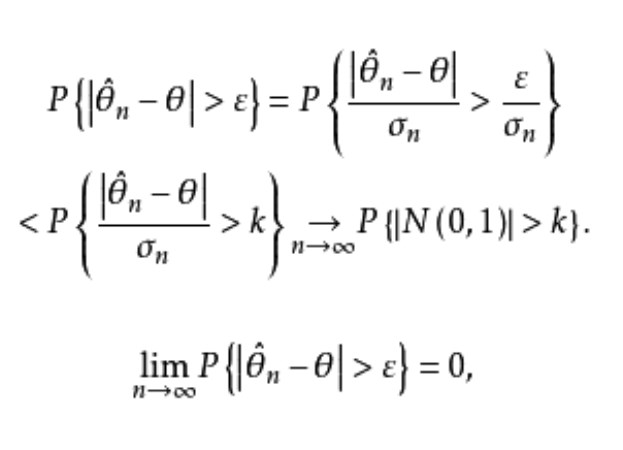

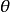
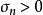
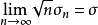
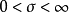
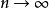
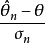

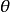
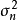


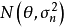


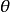

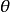
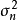
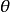
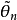
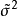
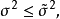

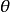

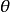
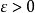
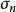

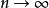
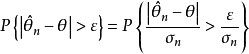
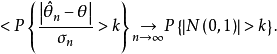
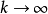
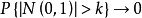
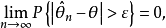

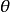
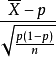
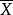
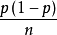
漸近正態估計也稱“相合漸近正態估計”,是當樣本容量n無限增大時,極限分布為常態分配的估計量。如樣本均值,樣本矩等均 為漸近正態估計;在相當廣泛的條件下,未知...
漸近正態性(asymptotic normality)估計量的一種漸近性質.設X=<X‑XZ,...}Xn}=是一個樣本,T<X)=<T,<X),Tz<X),...,T,<X)是參數B=<B‑BZ,.....
漸近正態估計量( asymptotic normal estimator)當樣本容量充分大時,極限分布為常態分配的估計量。如樣本均值、樣本矩。 ...
(2)最優漸近正態估計簡稱BAN估計。設X1、X2…Xn為從一總體中隨機獨立地抽出的樣本,總體分布具有密度函式或機率函式 ƒ(x,θ),滿足一定的正則條件,設g(θ)...
大樣本優良性準則有相合性、最優漸近正態估計和漸近有效估計等 [3] 。參數估計區間估計 區間估計(interval estimation)是依據抽取的樣本,根據一定的正確度與精確度...
萊卡姆(LeCam L.. ) 1953年證明,使估計量漸近方差小於克拉默-拉奧方差的值的集合的勒貝格測度為0。拉奧(RuoC. R.)證明,相合漸近正態估計量只有向極限分布的...
在金融工程領域,樣本的機率分布未必能夠呈現出嚴格的常態分配,往往呈現出有偏的漸進正態分布;在金融參數估計時,一般也需要通過對漸進分布的研究確定恰當的統計量,這...
在一定的條件下,這些偏度和峰度檢驗統計量具有漸近正態的優良性質和良好的功效。...此線形成數據所來自總體的累積分布函式的估計值。圖中會顯示總體參數的數字估計(...
2.3 估計的漸近正態性 182.4 假設檢驗 302.5 模擬研究 312.5.1 點估計的模擬研究 312.5.2 線性假設的檢驗 352.5.3 回歸變數的選擇 37 [1] ...
(2)構造雙變數Tobit模型一致的漸近正態的半參數估計量,得到該模型的一個可行性估計,克服最大似然估計和Amemiya估計量的缺陷。(3)設計實驗,對上述各估計量進行模擬...
GMM估計法具有一致性、漸近正態分布,有效率等性質。 [2] 廣義矩估計估計方法描述 編輯 假設我們有 個來自某統計模型的觀測值 ,並且我們知道下列 個矩(moment)...
對單參數最優估計給出了強相容性和漸近正態性,並且得到如此定義的最優準則與估計的漸近方差極小是一致的,即最優估計具有最小漸近方差。就我們這裡定義的多參數最...
[6]李永明 楊善朝.NA序列下經驗分布函式的漸近正態性及其套用[J].數學研究與評論,2006,26(3):457~[7]區詩德 黃敢基 楊善朝.歐式期權價值評估的非參數估計[J...
,αs的最小二乘估計,與其線性最小方差無偏估計一樣,具有相合性和漸近正態分布性質。最小二乘估計姙j(1≤j≤s)不涉及ω(t)的統計相關結構,是由數據x(1)...
文章主要研究了線性回歸模型在因變數缺失下的約束估計,基於完整數據方法和單點插補方法。我們給出了模型係數的兩種約束估計,並研究了估計量的漸近正態性.最後,我們...
5. 一類Pickands估計量漸近正態的充要條件(第二作者),《東北數學》,20046. 平穩高斯序列最大值與部分和的漸近聯合分布(第二作者),《工程數學學報》,2005...
