樣本矩是一個統計學術語,是指有一類常用的統計量是樣本的數字特徵,他們是模擬總體數字特徵構造的。樣本矩主要包括樣本均值、未修正樣本方差、樣本(修正)方差、樣本k階原點矩和樣本k階中心距。
基本介紹
- 中文名:樣本矩
- 外文名:sample moment
- 套用領域:數理統計
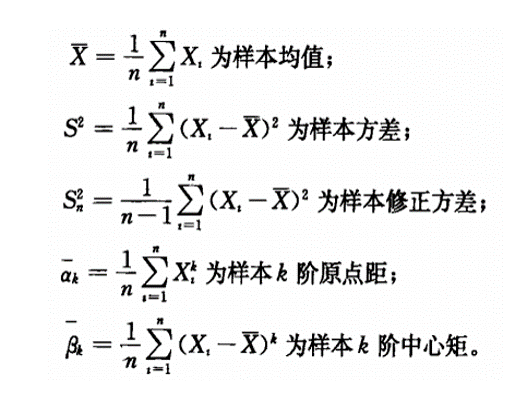
樣本矩是一個統計學術語,是指有一類常用的統計量是樣本的數字特徵,他們是模擬總體數字特徵構造的。樣本矩主要包括樣本均值、未修正樣本方差、樣本(修正)方差、樣本k階原點矩和樣本k階中心距。
矩估計,即矩估計法,也稱“矩法估計”,就是利用樣本矩來估計總體中相應的參數。首先推導涉及相關參數的總體矩(即所考慮的隨機變數的冪的期望值)的方程。然後取出一個樣本並從這個樣本估計總體矩。接著使用樣本矩取代(未知的)總體...
在隨機抽樣中,樣本統計量將依機率收斂於某個常數。這個常數又是分布中未知參數的一個函式。即在不知道分布的情況下,利用樣本矩構造方程(包含總體的未知參數),利用這些方程求得總體的未知參數。廣義矩估計是統計學和計量經濟學中常用...
往往通過總體矩(數字特徵)反映出來,因此若用樣本矩來替換總體矩,用樣本矩的函式替換相應的總體矩的函式,則可獲得總體參數 的估計量,這種估計方法稱為矩估計法。最大似然估計 最大似然估計又稱極大似然估計,它的基本思想是在給定...
樣本矩 設x1,x2,…,xn是一個大小為n的樣本,對自然數k,分別稱 為k階樣本原 點矩和k階樣本中心矩,統稱為樣本矩。許多最常用的統計量,都可由樣本矩構造。例如,樣本均值(即α1)和樣本方差 是常用的兩個統計量,前者反映...
①矩估計法。用樣本矩估計總體矩,從而得到總體分布中參數的一種估計。它的思想實質是用樣本的經驗分布和樣本矩去替換總體的分布和總體矩。矩估計法的優點是簡單易行, 並不需要事先知道總體是什麼分布。缺點是,當總體類型已知時,沒有...
1.了解總體、簡單隨機樣本、統計量、樣本均值、樣本方差及樣本矩的概念,其中樣本方差定義為 2.了解產生 變數、 變數和 變數的典型模式;了解標準常態分配、 t分布、F分布和分布得上側 分位數,會查相應的數值表.3.掌握正態總體的...
1 10 3隨機矩陣的矩23 1 11多元常態分配24 習題127 第2章數理統計的基本概念 29 2 1數理統計的一些基本概念29 2 2統計量和樣本矩31 2 2 1統計量的基本概念31 2 2 2樣本矩32 2 2 3順序統計量33 2 2 4經驗分布與格列汶...
4.2.2 隨機變數的矩 4.2.3 高斯隨機變數 4.3 聯合機率 4.3.1 二元分布 4.3.2 二元分布的矩 4.4 抽樣與估計的概念 4.4.1 樣本矩 4.4.2 估計值的置信區間 4.5 機率密度函式估計 4.5.1 χ2檢驗法的原理 4.5.2...
樣本的已知函式,其作用是把樣本中有關總體的信息匯集起來,是數理統計學中一個重要的基本概念。常用統計量有樣本矩、次序統計量、U統計量和秩統計量等。其中U統計量是W.霍夫丁於1948年引進的。統計量的充分性和完全性是兩個重要概念...
總體 個體 簡單隨機樣本 統計量 樣本均值 樣本方差和樣本矩 分布 分布 分布 分位數 正態總體的常用抽樣分布 考試要求 1.理解總體、簡單隨機樣本、統計量、樣本均值、樣本方差及樣本矩的概念,其中樣本方差定義為:2.了解 分布、 分布...
1.1.1 總體與樣本 1.1.2 統計量與樣本矩 1.2 抽樣分布與基本機率計算 1.2.1 常態分配 1.2.2 分布與偏分布 1.2.3 t分布與偏t分布 1.2.4 F分布與偏F分布 1.2.5 Weibull分布 1.3 點估計與估計量的...
