相似性所屬現代詞,是對兩個個體或部分之間的精細結構或性質等元素的一致性的評價。廣泛套用於數學、結構、模型、化學、語言等領域。
基本介紹
- 中文名:相似性
- 外文名:similarity
- 套用領域:數理、圖形、結構、化學、語言
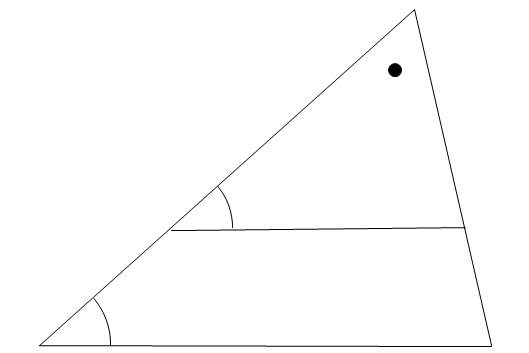
相似性所屬現代詞,是對兩個個體或部分之間的精細結構或性質等元素的一致性的評價。廣泛套用於數學、結構、模型、化學、語言等領域。
相似性所屬現代詞,是對兩個個體或部分之間的精細結構或性質等元素的一致性的評價。廣泛套用於數學、結構、模型、化學、語言等領域。數學中的相似性 幾何相似性 在歐幾里德幾何學中,兩個物體如果形狀相同,或者一個物體的形狀與另一個...
普遍性 自然界的相似性 在自然界中,大至宇宙星系之間,小至每個原子運動的形式,都存在著大量的相似之處。自然界的相似性 先看看宇宙星系。學過地理的人都知道,月球圍著地球轉,地球圍著太陽轉。當我們的目光遠離地球,鎖定茫茫的太陽...
相似性度量,即綜合評定兩個事物之間相近程度的一種度量。兩個事物越接近,它們的相似性度量也就越大,而兩個事物越疏遠,它們的相似性度量也就越小。相似性度量的給法種類繁多,一般根據實際問題進行選用。常用的相似性度是有:相關...
很多研究者認為區間假設檢驗是一種進行相似性檢驗適宜的統計方法。Jian提出了感官評價中區間假設檢驗的相似性檢驗方法。採用這種方法,無效假設是兩個處理間的差異等於或大於特定容許差異(△0),而備擇假設是小於特定容許差異:H0: ∣u1一...
相對於比較分子力場分析方法,相似性指數分析法(CoMSIA)是較晚建立的一種3D-QSAR方法。其理論基礎為具有相同作用機理的系列化合物的生物活性取決於配體和受體之間非鍵相互作用力強弱的變化,而作用力強弱的變化來自於每個配體化合物周圍分子...
論文相似性檢測統計服務打造人性化的設計,全面滿足用戶多方面、多層次的統計管理需求,套用起來得心應手,統計數據結果顯示一目了然。服務特色 報告支持分級別的賬號統計——按照主賬戶、子賬戶等分級別的賬號管理,方便管理者管理和統計。...
線上社交網路節點間相似性,描述了線上社交網路用戶之間的相似程度,根據不同的需求和定義,可以用相應的指標來進行度量,是線上社交網路分析研究的基礎。二、基於網路半結構信息定義節點相似性 1. 基於共同鄰居數的CN指標 從網路拓撲結構...
生理狀態相似性 除了環境方面的背景信息能影響學習者的記憶外,個人方面的背景信息如心境、意識水平甚至生理狀態同樣會影響記憶的效果。我們的情緒興奮時,能回想出許多愉快的事,心境不佳時能回想出許多不愉快的事。我們常常聽人這么說:...
相似性理論模型和引導搜尋理論模型以及特徵整個理論模型都屬於視覺搜尋的理論模型。Duncan和Humphreys在研究中發現:視覺搜尋效率在不同的作業任務、不同的研究條件下是有變化的,但這種變化沒有特徵整合理論描述的平行加工和系列加工那樣有明顯...
物種相似性 物種相似性是2006年公布的生態學名詞。定義 群落間或取樣間植物種類組成的相似程度或相異程度。出處 《生態學名詞》。
相位一致性可以被看做是體現局部結構信息重要性的一種無量綱。Liu等把相位一致性(PC)用於圖像質量評價,特徵相似性(FSIM)選取相位一致性信息作為第一個特徵。考慮到相位一致性不受對比度的影響,而對比度會影響圖像的質量,因此FSIM引入了...
相似性測度( similarity measure)是刻畫或說明匹配實體之間相似性程度的一種定量度量指標。一般說來,相似性程度是通過代價函式來計算的。在基於灰度的影像匹配中,常用的相似性測度包括相關係數測度、差平方和測度及差絕對和測度等。代價...
運動學相似性 運動學相似性(kinematic similarity)是2005年公布的航天科學技術名詞。公布時間 2005年,經全國科學技術名詞審定委員會審定發布。出處 《航天科學技術名詞》第一版。
非同源相似性(homoplasy)亦稱“同形質”。是指不同物種間並非由共同祖先遺傳而來的相似特性。不同有機體在形態和行為上的相似性有各自的根源,只有一種是從共同祖先那裡遺傳而來的,這就是同源。相似性也可能是不同物種適應一些相似的...
結構相似性 結構相似性(structural similarity)是2018年公布的生物物理學名詞。定義 生物大分子結構相似程度的度量。常用最佳結構重疊中對應殘基的α碳原子間距離的均方根偏差表示。出處 《生物物理學名詞》第二版。
化學相似性 化學相似性(chemical similarity)是2014年公布的藥學名詞。公布時間 2014年經全國科學技術名詞審定委員會審定發布。出處 《藥學名詞》第二版。
動力學相似性 動力學相似性(dynamic similarity)是2005年公布的航天科學技術名詞。公布時間 2005年,經全國科學技術名詞審定委員會審定發布。出處 《航天科學技術名詞》第一版。
相似性係數(similarity coefficient)是數量分類學術語。即以定量的形式描述分類單位之間相似性的數值,包括生物親緣關係。介紹 相似性係數數值的大小與相似性程度一致時,稱相親係數;與相似性程度不一致時,稱相異係數.通常使用的相似性係數...
網路文學作品相似性檢驗技術規範 《網路文學作品相似性檢驗技術規範》是2020年5月29日發布的一項行業標準。備案信息 備案號:73424-2020 備案月報: 2020年第6號(總第242號)
相似性指數 相似性指數是2021年公布的動物學名詞。定義 測量群落間或樣方間相似程度的指標。出處 《動物學名詞》。
similarity,英文單詞,名詞,作名詞時意為“類似;相似點”。單詞發音 英[ˌsɪməˈlærəti]美[ˌsɪməˈlærəti]短語搭配 cosine similarity餘弦相似性 ; 餘弦相似度 ; 向量空間餘弦相似度 ; 餘弦相似...
