熔化

熔化是指對物質進行加熱，使物質從固態變成液態的過程。它是物態變化中比較常見的類型。熔化需要吸收熱量，是吸熱過程。晶體有一定的熔化溫度，叫做熔點。非晶體沒有一定的熔化溫度。熔化的逆過程是凝固。

基本介紹

• 中文名：熔化
• 外文名：melt
• 定義：物質由固態變成液態的變化過程
• 拼音：rong hua
• 理論：分子內部原子的振動（外界因素）
• 套用：晶體的特徵表現

定義

熔化是通過對物質加熱，使物質從固態變成液態的一種變化過程。熔化需要吸收熱量，是吸熱過程。

冰

晶體有一定的熔化溫度，叫做熔點，在標準大氣壓下，與其凝固點相等。晶體吸熱溫度上升，達到熔點時開始熔化，此時溫度不變。晶體完全熔化成液體後，溫度繼續上升。熔化過程中晶體是固、液共存狀態。

非晶體沒有一定的熔化溫度。非晶體熔化過程與晶體相似，只不過溫度持續上升，需要持續吸熱。

熔點是晶體的特性之一，不同的晶體熔點是不同的。

凝固是熔化的逆過程。實驗表明，無論是晶體還是非晶體，在凝固時都要向外放熱。晶體在凝固過程中溫度保持不變，這個溫度叫晶體的凝固點（solidifying）。同一晶體的凝固點與熔點相同。非晶體沒有凝固點和熔點。

晶體熔化的條件：

1. 溫度達到熔點；
2. 達到熔點後繼續加熱。（吸熱）

熔化理論

對於二維體系，熔化理論已經相當成熟，在晶體和液體之間存在一種中間物稱為六角相，這種中間物有一定的取向，但沒有平移有序。然而，在三維體系中，熔化的理論仍然沒有得到明確的建立。在早期的一種關鍵方法中，Lindemann引提出當原子振動的均方根振幅達到原子間距的臨界分數時，熔化就會發生。由於加熱過程中晶體的剪下模量減小，Born提出只要這些模量中的一個減小到零，熔化就會發生，這可以被認為是剛性失穩或機械熔化。在這種變化中，整個晶格點陣均勻連續地變為液體。Lindemann和Born本來打算將熔化描述為我們平常所觀察的那樣，但是實際在固體中的熔化是不均勻的。通常熔化開始於晶體表面，然後向內部傳播。在熔化溫度，晶體和液體共同存在，並且它們之間存在明確的界面，固體是剛性的，彈性模量不為零。通常表面熔化開始的時候不需要形核能壘，因此熔化過程中通常沒有過熱。然而，表面熔化可以被抑制，例如通過塗覆一層熔點更高的材料，然後發現晶體的內部可以充分的過熱。我們很想知道是什麼原因限制了可以達到的過熱度。在很多領域，
過熱度及其影響引起了很大的興趣，例如在半熔的岩漿體，雷射強烈輻照效應，以及電線的電熔爆等。

Born的剛性失穩判據對固體的過熱建立了一個可能的限制條件。基於焓、熵或者是過熱晶體的體積等於液體的體積等均勻熔化的其他類型的失穩判據也被提出。當溫度高於平衡熔化溫度的兩倍時，這些類型的失穩出現。Lu和Li首次分析了晶體中內在熔化的形核動力學，指出在發生失穩之前充分加熱，形核可以發生。當今普遍接受的觀點是：正是由於晶體內液體的形核，而不是晶體的完全失穩，這就建立了過熱的極限。由於熔化的開始是動力學限制的，因此過熱度受加熱速度限制。

Lu和Li的原始分析採用了均質形核的經典理論。雖然正確地預測了熔化過程中的體積變化產生了大的形核能壘，這對完整的熔化形核分析還相差很遠。晶體中的缺陷為異質形核提供了可能性。我們仍然對經典理淪之外的討淪感興趣。由於很難長時間維持過熱狀態，因此對過熱的定量觀察比對過冷的研究少得多，許多研究都是基於原子模擬。

熔化焓和熔化熵

在一定溫度、壓力下，純物質熔化（晶體轉變為液態）的過程中體系所吸收的熱（即過程的熱效應）。等於過程前後體系焓的增量，故現又稱為熔化焓。手冊中查到的標準（摩爾）熔化焓，是指在標準狀態下，1mol純物質完全熔化時焓的增量，用符號△_fusH_θm表示。例如，冰在其熔點（0℃）的標準熔化焓為6.008千焦/摩。

Lai等在測定了Sn納米粒子熔點的同時也測定了它的熔化焓Δ_fusH_m隨粒度的變化。發現當粒度減小到一定程度後，Δ_fusH_m比其粗晶值（58.9 J·g^-1）降低70%。按照經典熱力學處理方法，熔化焓常被視為一個常數。直到20世紀90年代，計算機MD模擬發現，Au原子團的Δ_fusH_m隨粒度降低而減小。Lai等利用Hanszen的熔融模型，求得了熔點和熔化焓隨顆粒度變化的函式關係。按照這一模型，固體粒子被一層薄薄的液層包圍，其熔點溫度等於固態球核與一定厚度的液層達到平衡時的溫度。如圖所示，半徑為r=R₀，表面自由能為γ_s-g的固體粒子熔融變為半徑為r_s的固體核心，被厚度為t₀=r-r_s的薄液層完全潤濕，液層表面自由能為γ_l-g，固液界面自由能為γ_s-l。

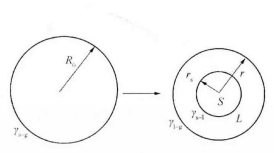Hanszen的熔融模型

假定固體核心如同塊狀物質，其單位體積熔化潛熱與溫度無關，按照經典熱力學方法，熔點溫度T_m。可以表示為：

T₀ -T_m=2T₀/Δ_fusH₀ [γ_s-l/ρ(r-t₀)+(γ_l-g/r+Δp/2)(1/ρ₁-1/ρ₂) ]

式中：T₀和Δ_fusH₀為塊狀本體物質的熔點和熔融焓；r是粒子的半徑；t₀是熔化溫度下內部固體心與包裹的液態薄層達平衡時液態薄層的臨界厚度．是一個可以通過擬合實驗數據而得到的調節參數；γ為表面自由能；ρ為密度；△p為蒸氣壓差，即半徑為r的液滴的表面蒸氣壓與，r=∞的平面液體蒸汽壓的壓差。由於兩者相差很小，Δp的貢獻可以忽略。

另外，熔化熱的表達式為： Δ_fusH_m = Δ_fusH₀（1-t₀/r）³

對於Sn納米粒子，理論計算與實驗測定結果基本吻合。類似的報導還有Eckert等測定的納米晶Al的熔化焓和熔點溫度隨粒度的變化。

熔化熵類似於熔化焓，隨粒度減小而降低。下圖對比了納米Sn的熔化焓Δ_fusH_m 和熔化熵Δ_fusS_m 隨粒度變化。無論是金屬、半導體，還是有機晶體，都可以觀察到這一現象。

熔化焓和熔化熵計算值對比

常見晶體的熔點

晶體的熔點（在1標準大氣壓下）

物質	熔點（℃）	物質	熔點（℃）	物質	熔點（℃）
金剛石	3550	金	1064	冰	0
鎢	3410	銀	962	固態水銀	-39
純鐵	1535	鋁	660	固態酒精	-117
各種鋼	1300-1400	鉛	327	固態氮	-210
各種鑄鐵	1200	錫	232	固態氫	-259
銅	1083	硫代硫酸鈉（海波）	48	固態氦	-272

相關知識

1、物質熔化需要吸熱（吸外界或自身的熱量）。

非晶體

2、固體根據熔化特點分為晶體與非晶體

（1）晶體：具有固定的熔點（熔化時溫度保持不變）；

（2）非晶體：不具有固定的熔點（熔化時溫度持續上升）。

3、一般情況，對於同一晶體的熔點與大氣壓有關。壓強越大，熔點越高；壓強越小，熔點越低。但是水除外，壓強越大，熔點越低；壓強越小，熔點越高。所以水有著不同於其它純態物質的單元系相圖，它的固液線的斜率是負的，這一點與其它物質非常不同。

擴展閱讀

1888年，在奧地利有一個叫萊尼茨爾的科學家，合成了一種奇怪的有機化合物，它有兩個熔點。把它的固態晶體加熱到145℃時，便熔成液體，只不過是渾濁的，而一切純淨物質熔化時卻是透明的。如果繼續加熱到175℃時，它似乎再次熔化，變成清澈透明的液體。後來，德國物理學家列曼把處於“中間地帶”的渾濁液體叫做液晶。它好比是既不像馬，又不像驢的騾子，所以有人稱它為有機界的騾子。液晶自被發現後，人們並不知道它有何用途，直到1968年，人們才把它作為電子工業上的的材料。

該熔化非彼溶化，該熔化是指對晶體類的物質加熱，變成高溫度的液體。