三維歐氏空間由二參變數(u,v)定義的具有二個自由度的直線全體{l(u,v)}稱為直線匯或簡稱線匯,各直線稱為光線。這方面理論發端於1828、1830年W.R.哈密頓的研究。
焦曲面(focal surface)是指由線匯確定的一種特殊曲面。經過線匯的任何一條射線,一般可引兩個可展曲面。各射線與各可展曲面的脊線有一個切點,稱為該射線的焦點。
基本介紹
- 中文名:焦曲面
- 外文名:focal surface
- 領域:數學
- 性質:特殊曲面
- 主要元素:線匯
- 子類:雙葉焦曲面
概念
線匯
可展曲面
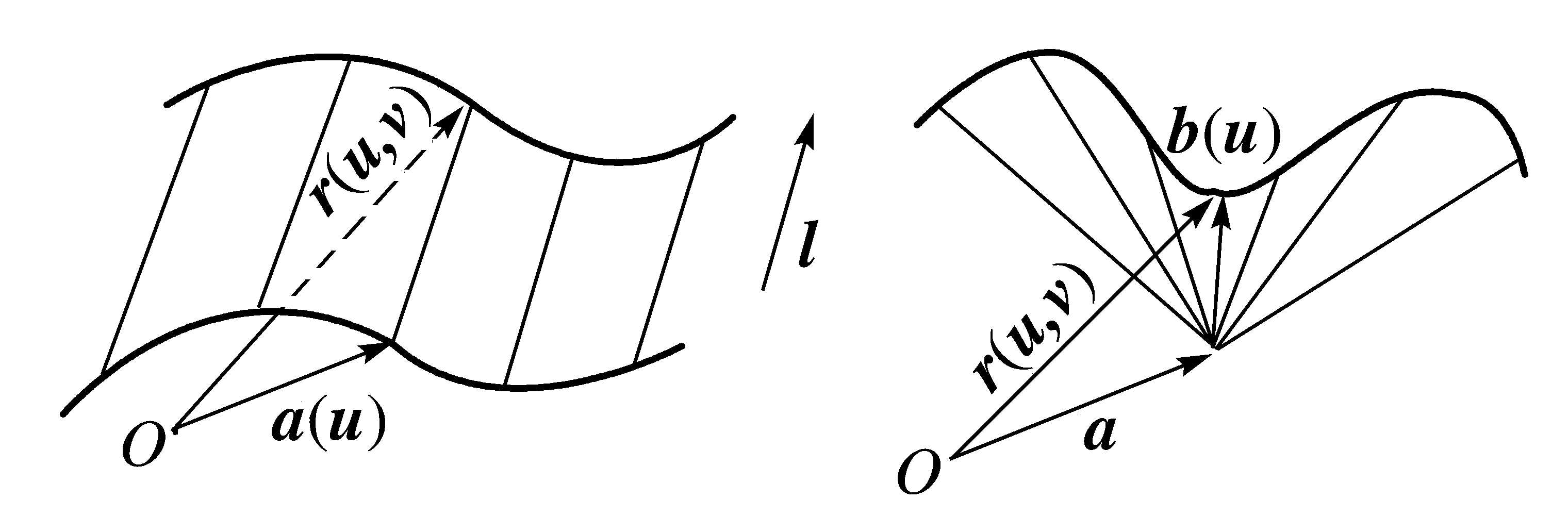

三維歐氏空間由二參變數(u,v)定義的具有二個自由度的直線全體{l(u,v)}稱為直線匯或簡稱線匯,各直線稱為光線。這方面理論發端於1828、1830年W.R.哈密頓的研究。
焦曲面(focal surface)是指由線匯確定的一種特殊曲面。經過線匯的任何一條射線,一般可引兩個可展曲面。各射線與各可展曲面的脊線有一個切點,稱為該射線的焦點。

三維歐氏空間由二參變數(u,v)定義的具有二個自由度的直線全體{l(u,v)}稱為直線匯或簡稱線匯,各直線稱為光線。這方面理論發端於1828、1830年W.R.哈密頓的研究。焦曲面(focal surface)是指由線匯...
主要分為如下三個部分:.1..研究Minkowski空間中一般曲線及其對偶曲線, 焦曲面的奇點和性質問題, 並從統一的視角來刻畫三種特殊類型曲線(即類空型, 類光型和類時型)之間的區別和聯繫..2..揭示Minkowski空間中類光曲面及相關對象的奇...
在這一理論中研究焦曲面和可展曲面、焦點等。簡介 射影微分幾何學(projective differential geometry)從屬於射影變換群。其思想來源於C.F.克萊因1872年的著名演說“埃朗根綱領”,在那裡將幾何學歸結為可逆變換群的幾何不變數理論加以分類。
表示一個二次共焦曲面,曲面的大小形狀與u有關。u在不同區間內變化時,它表示不同大小形狀的共焦曲面。為此。我們可按u在不同區間的變化來考查曲面的大小形狀。(1)當u=0時,則 表示橢球面,其半主軸長度為a,b和c。(2)...
一、 直紋面與可展曲面 二、 旋轉曲面 三、 平行曲面,曲面的焦曲面 四、 偽球面與Sine?Gordon方程 五、 B?cklund變換 §2.7歐氏空間的變換群 一、 變換群 二、 線性變換群GL(n)三、 線性變換群的某些特殊子群 四、 變換...
