乘法交換律是一種計算定律,兩個數相乘,交換因數的位置,它們的積不變,叫做乘法交換律,用字母表示a×b=bxa。一般在只有乘法的算式計算中,一般是按照從左到右的順序進行計算,有時候,採用乘法交換律可以進行簡便運算。
基本介紹
一般計算規則
定義
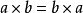



作用
套用
運算例題
簡單計算

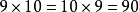
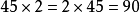

簡便運算
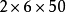
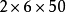


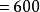
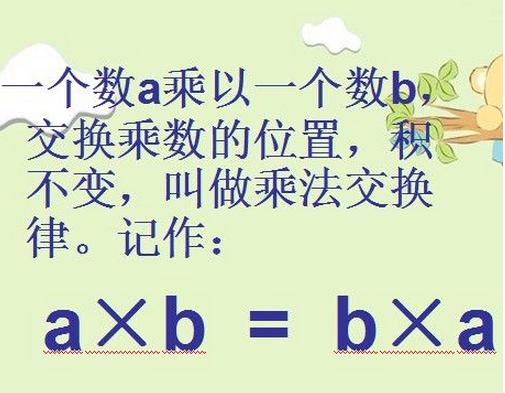
乘法交換律是一種計算定律,兩個數相乘,交換因數的位置,它們的積不變,叫做乘法交換律,用字母表示a×b=bxa。一般在只有乘法的算式計算中,一般是按照從左到右的順序進行計算,有時候,採用乘法交換律可以進行簡便運算。
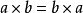




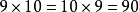
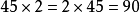

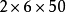
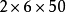


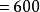
乘法交換律是一種計算定律,兩個數相乘,交換因數的位置,它們的積不變,叫做乘法交換律,用字母表示a×b=bxa。一般在只有乘法的算式計算中,一般是按照從左到右的...
乘法結合律是乘法運算的一種,也是眾多簡便方法之一。三個數相乘,先把前兩個數相乘,再和另外一個數相乘,或先把後兩個數相乘,再和另外一個數相乘,積不變。...
乘法運算定律,也叫乘法的性質,有交換律,結合律, 分配律,套用這些運算定律,可以使部分乘法題計算簡便。...
數學交換律為數學用語,給定集合S上的二元運算·,如果對S中的任意a,b滿足,則稱滿足交換律。...
加法交換律是數學計算的法則之一。指兩個加數相加,交換加數的位置,和不變。交換律是二元運算的一個性質,意指在一個包含有二個以上的可交換運運算元的表示式,...
在群上再裝備另一種乘法, 則發展成為“環”, 兩種乘法中的一種可以視為傳統意義上的加法,因此要求滿足分配律和交換律;但是另一種“乘法”卻不要求交換律。...
滿足乘法交換律的方陣稱為可交換矩陣,即矩陣A,B滿足:A·B=B·A。高等代數中可交換矩陣具有一些特殊的性質。下面所說的的矩陣均指n 階實方陣。...
運算律是通過對一些等式的觀察、比較和分析而抽象、概括出來的運算規律。既是重要的數學規律,也是數學運算固有的性質。包括加法交換律和結合律、乘法交換律和結合律...
被乘數是數學術語,指四則運算的乘法中被乘的數字,又叫因數,一般來說放在算式的前面。小學生初學乘法時,年齡小、接受能力差,又沒有乘法交換律的知識基礎,而乘法的...
加法運算分為:加法交換律和加法結合律乘法運算分為:乘法交換律、乘法結合律和乘法分配律除法性質:商不變減法性質: 差不變小數性質
這裡,從a、b得到c的運算就叫乘法,a叫乘數(因數),b也叫乘數(因數)。例如:5×5=25乘運算定律 編輯 乘法交換律兩數相乘,交換位置其結果不變,即a×b=b×a。...
它可以改變乘法運算當中的運算順序,在日常生活中乘法結合律運用的不是很多,主要是在一些較複雜的運算中起到簡便的作用。簡便計算乘法交換律 ...
=m·n+(m·k+m)=m·n+(m+m·k)=(m·n+m)+m·k(加法結合律、交換律)=m·n'+m·k (乘法定義), 因此結論對n'也成立, 由數學歸納原理知, 乘法...
加法:(加法交換律) (加法結合律)(近似數) 乘法:(乘法交換律)(乘法結合律)(乘法分配律)(乘法分配律變化式(四個)) 減法:(減法的基本性質)(近似數) 除法:(...
