混合線性模型(mixed linear model)是一種方差分量模型。在方差分量模型中,把既含有固定效應,又含有隨機效應的模型,稱為混合線性模型。
基本介紹
- 中文名:混合線性模型
- 外文名:Mixed linear model
- 所屬學科:數學
- 所屬領域:統計學(線性模型)
- 特點:既含有固定效應,又含有隨機效應
基本介紹
混合線性模型的結構

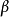

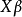
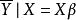

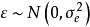

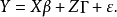
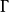
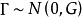



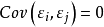


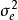
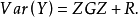
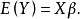
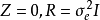

混合線性模型(mixed linear model)是一種方差分量模型。在方差分量模型中,把既含有固定效應,又含有隨機效應的模型,稱為混合線性模型。

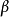

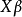
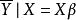

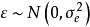

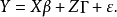
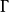
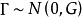



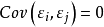


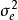
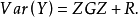
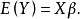
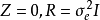
混合線性模型(mixed linear model)是一種方差分量模型。在方差分量模型中,把既含有固定效應,又含有隨機效應的模型,稱為混合線性模型。...
混合模型(hybrid model)是幾種不同模型組合而成的一種模型。它允許一個項目能沿著最有效的路徑發展。也可定義為由固定效應和隨機效應(隨機誤差除外)兩部分組成的...
那么因變數自身的“現在”與“過去”,因變數與各自變數的“現在”與“過去”都可能存在統計依賴關係。為此需要建立混合線性回歸模型 [1] 。...
本書研究了線性混合效應模型的影響分析問題,將近兩年剛剛發展起來的Q函式方法全面系統地套用於該模型的統計診斷,對6種協方差結構的模型給出了Cook型診斷統計量,並...
混合計算機模型(hybrid computational models)是由計算機與其所控制的物理部件構成的,具有既隨時間連續變化的變數又受事件驅動的離散變數的系統的數學模型。在已有的計算...
多重混合線性張量模型及其參數估計[J]. 蘇州科技大學學報(自然科學版),2017,34(01):42-48. 3. 張慶紅,程國建. 基於張量積樣條混合算法的計算機建模可視化[J]....
《線性混合效應模型引論》是2013年出版的圖書,作者是吳密霞。...... 《線性混合效應模型引論》系統闡述了線性混合效應模型的基本理論、方法和套用,全書共12章。第1...
《混合效應模型在林業建模中的套用》是關於線性和非線性混合效應模型理論、方法及其在林業建模上套用的專著。內容主要介紹單水平和多水平統計模型。將單水平混合效應...
中文名稱 混合模型方程組 英文名稱 mixed model equations;MME 定義 由亨德森(C.R. Henderson)於1953年推導的,以混合模型為基礎建立的線性方程組。對這種方程組...
《線性和廣義線性混合模型及其統計診斷》是科學出版社2013年出版的圖書,作者是費宇、陳飛等。...
1 三段論介紹 2 推理研究 ▪ 操作模型 ▪ 空間表象模型 ▪ 語言模型 ▪ 混合模型 線性三段論三段論介紹 編輯 是依據有序事物間的關係進行的推理,它...
協方差分析模型(covariance analysis model)是方差分析模型和線性回歸模型的一種“混合”。由於協方差分析模型中不是所有的自變數都為可控變數,故自變數分為不可控的...
《線性模型的預測理論及其套用》是2011年水利水電出版社出版的圖書,作者是徐禮文。本書所論述的主要內容是作者及其合作者線上性統計模型預測這一領域近些年的研究成果,...
《廣義GAMMA分布簇廣義線性混合模型理論與套用》是2014年對外經濟貿易大學出版社出版書籍,作者是謝遠濤 楊娟。...
重要方法,由自回歸模型(簡稱AR模型)與移動平均模型(簡稱MA模型)為基礎“混合”...許多譜估計中,僅能得到模型的輸出序列{x(n)},這時,參數估計是非線性的,難以...
基於混合線性模型的複合區間作圖法 朱軍(1998) 提出了用隨機效應的預測方法獲得基因型效應及基因型與環境互作效應,然後再用區間作圖法或複合區間作圖法進行遺傳主效應...
