重言式

重言式（Tautology ）又稱為永真式，它的漢語拼音為：[Chóng yán shì]，是邏輯學的名詞。命題公式中有一類重言式。如果一個公式，對於它的任一解釋下其真值都為真，就稱為重言式（永真式）。數理邏輯旨在利用有限的公理推出儘可能多的重言式，除此之外，重言式在計算機詞法分析領域也具有重要套用。

基本介紹

• 中文名：重言式
• 外文名：Tautology 
• 別名：永真式
• 拼音：Chóng yán shì
• 類別：命題公式
• 所屬學科：離散數學、邏輯學

定義

給定一命題公式，若無論對分量作怎樣的指派，其對應的真值永為T（True），則稱該命題公式為重言式或永真公式。

顯然由聯結詞∨、∧、→和聯結的重言式仍是重言式。

一個公式，如有某個解釋I0, 在I0下該公式真值為真, 則稱這公式是可滿足的。P∨Q當取I0 = (T, F)即P = T, Q = F時便有P∨Q = T, 所以是可滿足的。重言式當然是可滿足的。

另一類公式是矛盾式（永假式或不可滿足的）。如果一個公式，對於它的任一解釋I下真值都是假，便稱是矛盾式。如P∧P就是矛盾式。

不難看出這兩類公式間有如下關係:

1. 公式A永真， 若且唯若永假。

2. 公式A可滿足, 若且唯若非永真。

3. 不是可滿足的公式必永假。

4. 不是永假的公式必可滿足。

永真式與永假式互為否定式

相關定理

定理1： 任何兩個重言式的合取或析取，仍然是一個重言式。

定理2：一個重言式，對同一分量都用任何公式置換，其結果仍為一重言式。

定理3：設A,B為兩個命題公式，A和B邏輯等價若且唯若雙條件命題“A若且唯若B”成立。

定理4：設A,B,C為合式公式，若A蘊含B且A是重言式，則B也是重言式。

定理5：若A蘊含B，B蘊含C，則A蘊含C，即蘊含關係是傳遞的。

離散數學領域

重言式判定

在布爾代數中發現重言式的最簡單的方法是使用真值表。但是，隨著涉及到的變數的數目的增長，真值表的大小成 2 的冪次增長，這使它不利於四個或更多變數的重言式，這時簡化和代數變得更有用。

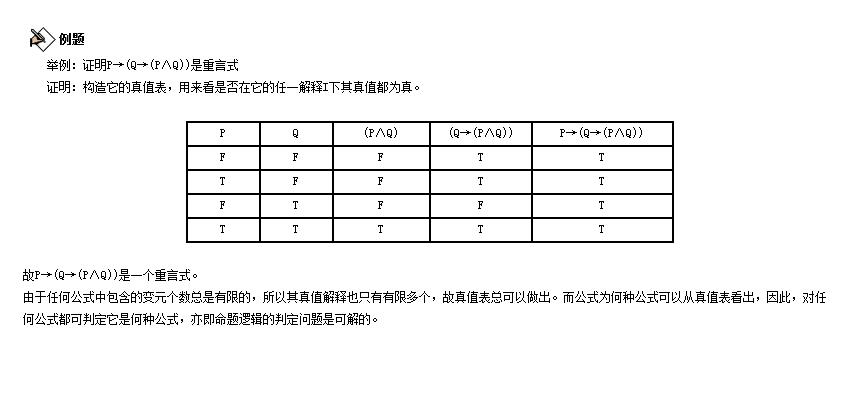利用真值表判定重言式

在對命題邏輯代數化表示的基礎上,通過解多項式方程組,對命題公式進行等價變換、演繹推理。用有理數域上的多項式組替代命題公式,利用純代數的方法給出命題公式的重言式和矛盾式的證明。

代入規則

A是一個公式, 對A使用代入規則得公式B，若A是重言式，則B也是重言式。

為保證重言式經代入規則仍得到保持，要求:

1. 公式中被代換的只能是命題變元（原子命題）,，而不能是複合命題。

2. 對公式中某命題變項施以代入，必須對該公式中出現的所有同一命題變項代換同一公式。

重言式示例

• “1+1=2”
  
• “所有的三角形都有三個邊。”
  
• “四足動物就是有四隻腳的動物。”
  
• “所有的單身漢都沒有結婚。”（單身漢之定義即是：尚未結婚的男人）
  
• “小明很受女孩子歡迎，因為他有女性緣。”（女性緣的意思即是受女生歡迎，因為小明受女生歡迎，才被人們認為有女性緣）
  
• “西湖的水裡要么有魚要么沒有魚。”
  
• “要發生的終究是要發生的。”
  

離散例題

(p^(p->q))->q，證明其為重言式，利用真值表證明如下：

p	q	p->q	p^(p->q)	(p^(p->q))->q
0	0	1	0	1
0	1	1	0	1
1	0	0	0	1
1	1	1	1	1

最後一列真值永為1，即說明此命題公式為重言式。

計算機領域

重言式作為即為邏輯詞，在計算機領域具有廣泛套用。在自然語言處理的詞法分析領域，重言式經常被用作邏輯判斷的準則。重言式在，計算機領域中也經常被推廣為廣義重言式，且其經常與離散數學中的二值邏輯模糊蘊涵運算元結合使用，其在近年來已成功套用於模糊控制、近似推理、詞計算、模糊圖像處理等諸多領域,引起了學者們的廣泛關注.其中,與蘊涵運算元相關的廣義重言式已經成為當前研究的熱點.目前,人們逐漸意識到廣義重言式在模糊邏輯的理論及套用中發揮的重要作用。