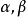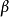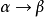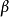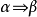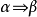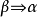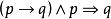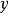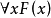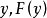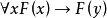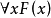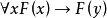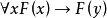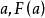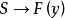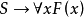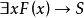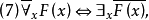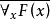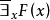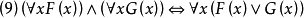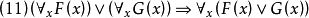普遍有效公式(universally valid formula)亦稱永真公式或恆真公式，是一種基本公式。普遍有效是數理邏輯用語，狹謂詞演算的一個公式是普遍有效的，若且唯若：對任何個體域，用任一個體常項代人其中的個體變項，用任一命題常項代人其中的命題變項，並且用任一特定的謂詞常項代人其中的謂詞變項，其結果總是真的。一公式普遍有效時，稱為普遍有效公式。狹謂詞邏輯中的普遍有效公式往往顯示了一個邏輯規律。例如：(∀x)(F(x)∨¬F(x))表示排中律。(∀x)A(x)→(∃x)A(x)表示全稱蘊涵存在。命題邏輯中的普遍有效公式就是重言式。
基本介紹
- 中文名：普遍有效公式
- 外文名：universally valid formula
- 別稱：永真公式、恆真公式
- 所屬學科：數學（數理邏輯）
- 相關概念：重言式，謂詞演算公式等
基本介紹,一些重要的普遍有效公式,
基本介紹
由謂詞填式或命題變元，利用真值函式和量詞所構成的式子叫做謂詞演算公式。
如果謂詞演算公式中，不論用任何特定的命題代入其中的命題變元，不論對什麼個體域，不論用任何特定個體代入其中的個體變元，並且用任一特定的謂詞代入其中的謂詞變元，其結果總是真的(或者假的)則稱這個謂詞演算公式為永真公式(或者永假公式)。渭詞演算永真公式又叫做普遍有效公式。
設
是兩個謂詞演算公式，如果“
”是一個永真公式，則稱
與
等價，記為
。如果“
”是一個永真公式，則稱永真蘊涵，記為
，顯然若且唯若且
。
普遍有效公式的獲得，有的可以從命題演算公式中的永真公式(即重言式)得到。如果謂詞演算公式中包含量詞，且出現的變元都是約束變元，那么這個謂詞演算公式就是一個命題，因此用它置換命題演算永真公式中的命題，得到的是普遍有效公式。例如，由
，得
。還有的可以用謂詞填式置換命題演算永真公
式中的命題而得到。例如，由
，得
。又如，由
得
。
除此之外，普遍有效公式還可以從量詞的意義得出。
用以上諸法得到的普遍有效公式，如果是永真蘊涵式，那么相應地，就得到了正確的推理形式，即推理格式。
一些重要的普遍有效公式
下面給出一些重要的普遍有效公式，並給予必要的說明。
如果
取真值，那么對任意取定的個體變元
都真，所以
為真。
如果取假值，則根據蘊涵的定義，必真。
因此，無論何種情形，永真，即
。
如果對於某一個體
真，則
必真，所以
真;
如果
假，則根據蘊涵的定義，必真。
因此
。
如果任選定個體y，而由某前提S能推出y具有某個性質F(相當於
，那么由同樣的前提S就能夠推出所有個體都具有這個性質F(相當於
)。
例如，要推證“線段的垂直平分線上的所有的點都與線段兩端等距”，推證的方法是：在垂直平分線上任取定一點，證明這點與線段兩端等距”。這是因為，如果能夠證明垂直平分線上任意取的一點有此性質，那么就證明了上面所有的點都有此性質。這裡說y是任選的個體，就是說y的選擇應當與前提S無關，即指“S中不含作為自由變元的y”；若S中含有作為自由變元的y，則y的選擇就與前提S有關了。
如果能任選定個體y，具有某性質F，它蘊涵S(相當於
)，那么，必能有個體具有性質F，它蘊涵S (相當於
)，這裡說y為任選的個體，就是指y的選擇應當與S無關，它反映了“S中不含作為自由變元的y”。
如果所有的x，都使F(x)真，那么必有x，使F(x)真。
對於約束變元而言，x可以改為y或其他字母，但不能與已在式中用的字母重複。
並非所有x均使F(x)真，等價於有x使F(x)不真。
不存在x使F(x)真，等價於所有的x都使F(x)不真。
所有x都使F(x)真，且所有x都使G(x)真，等價於所有x都使F(x)與G(x)均真。
有x使F(x)真，或有x使G(x)真，等價於有x使F(x)或G(x)真。
如果所有x都使F(x)真，或所有x都使G(x)真，那么，
所有x都使F(x)或G(x) 真。注意：反過來未必成立!
如果有x使F(x)和G(x)均真，則必定有x使F(x)真且有x使G(x)真。注意: 反過來未必成立!
