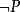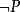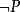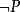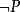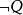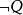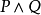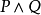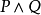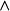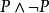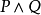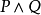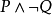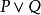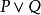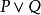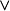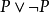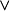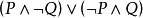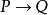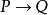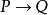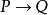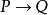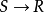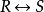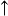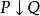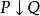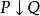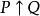聯結詞亦稱命題聯結詞，命題邏輯的基本概念之一，指由已有的命題構造出新命題所用的詞語。例如，由命題“二加三等於五”和“蘇格拉底是人”可以構造出新命題“二加二等於五並且蘇格拉底是人”，在這裡，“並且”是聯結詞，又例如，由命題“蘇格拉底是人”可以構造出它的否命題“蘇格拉底不是人”，在這個否命題中，“不”是聯結詞，最重要的聯結詞有否定“非”，合取“且”，析取“或”，蘊含“如果……則……”以及等價“若且唯若”。
基本介紹
- 中文名：聯結詞
- 外文名：connective
- 別名：邏輯聯結詞、命題聯結詞等
- 屬性：命題邏輯的基本概念之一
- 所屬學科：數理科學
簡介,否定聯結詞,合取聯結詞,析取聯結詞,條件聯結詞,雙條件聯結詞,異或聯結詞,與非聯結詞,或非聯結詞,
簡介
一個複合命題，不論其構成多么複雜，一般都可以分析出構成該命題的原子命題。下面介紹幾種常用的邏輯聯結詞(Logical Connectives)，分別是“非”(否定聯結詞)、“與”(合取聯結詞)、“或”(析取聯結詞)、“若…則…”(條件聯結詞)、“…若且唯若…”(雙條件聯結詞)，通過這些聯結詞可以把多個原子命題複合成一個複合命題。此外，還介紹了三種，分別是異或聯結詞、與非式、或非式。
否定聯結詞
定義1 設P為一命題，P的否定(Negation)是一個新的命題，記為(讀作非P)。規定若P為T(真)，則
為F(假)：若P為F，則 為T。 的取值情況依賴於P的取值情況，真值表如表1所示。
P | 非P |
F | T |
T | F |
在自然語言中，常用“非”、“不”、“沒有”、“無”、“並非”等來表示否定。
例1 P：北京是中國的首都。 ：北京不是中國的首都。
P是真命題， 是假命題。
Q：所有的海洋動物都是哺乳動物。
：不是所有的海洋動物都是哺乳動物。
Q為假命題， 為真命題。
合取聯結詞
定義2設P、Q為兩個命題，P和Q的合取(Conjunction)是一個複合命題，記為
(讀作P與Q)，稱為P與Q的合取式。規定P與Q同時為T時， 為T，其餘情況下， 均為F。
聯結詞“
”的真值表如表2所示。
P | Q | P與Q |
F | F | F |
F | T | F |
T | F | F |
T | T | T |
顯然
的真值永遠是假，稱為矛盾式。在自然語言中，常用“既…又…”、“不但…而且…”、“雖然…但是…”、“一邊…一邊…”等表示合取。
例2 (1)今天颳風又下雨。
設P：今天颳風。Q：今天下雨。則(1)可表示為 。
(2)1+1=2且太陽從西方升起。
設P：1+I=2。Q：太陽從西方升起。則(2)可表示為 。
(3)張三雖然聰明但不用功。
P：張三聰明。Q：張三用功。則(3)可表示為
。
需要注意的是，在自然語言中，命題(2)是沒有實際意義的，因為P與Q兩個命題是互不相干的，但在數理邏輯中是允許的，數理邏輯中只關注複合命題的真值情況，並不關心原子命題之間是否存在著內在聯繫。
析取聯結詞
定義3 設P、Q為兩個命題，P和Q的析取(Disjunction)是一個複合命題，記為
(讀作P或Q)，稱為P與Q的析取式。規定若且唯若P與Q同時為F時， 為F，否則 均為T。
析取聯結詞“
”的真值表如表3所示。
P | Q | P或Q |
F | F | F |
F | T | T |
T | F | T |
T | T | T |
顯然
的真值永遠為真，稱為永真式。
析取聯結詞“
”與漢語中的“或”二者表達的意義不完全相同，漢語中的“或”可以表達“排斥或”，也可以表達“可兼或”，而從析取聯結詞的定義可以看出，“ ”允許P、Q同時為真，因而析取聯結詞“ ”是可兼或。
例3 (1)小王愛打球或跑步。
(2)他身高1.8m或1.85m。
(1)為可兼或，(2)為排斥或。
設P：小王愛打球。Q：小王愛跑步。則(1)可表示為 。
設P：他身高1.8m。Q：他身高1.85m。則(2)可表示為
。
條件聯結詞
定義4 設P、Q為兩個命題，P和Q的條件(Conditional)命題是一個複合命題，記為
(讀作若P則Q)。其中P稱為條件的前件，Q稱為條件的後件。規定若且唯若前件P為T，後件Q為F時， 為F，否則 均為T。
條件聯結詞“
”的真值表如表4所示。
P | Q | 若P則Q |
F | F | T |
F | T | T |
T | F | F |
T | T | T |
在自然語言中．常會出現的語句如“只要P就Q”、“因為P所以Q”、“P僅當Q”、“只有Q才P”、“除非Q才P”等都可以表示為“ ”的形式。
例4 (1) 如果雪是黑色的，則太陽從西方升起。
(2) 僅當天氣好，我才去公園。
對於(1)，設P：雪是黑色的。Q：太陽從西方升起。則(1)可表示為 。
(2)設R：天氣好。S：我去公園。則(2)可表示為
。
雙條件聯結詞
定義5 設P、Q為兩個命題，其複合命題
稱為雙條件(Biconditional)命題， 讀作P當R僅當Q。規定若且唯若P與Q真值相同時， 為T，否則 均為F。
雙條件聯結詞“ ”的真值表如表5所示。
P | Q | P若且唯若Q |
F | F | T |
F | T | F |
T | F | F |
T | T | T |
例5 雪是黑色的若且唯若2+2>4。
(2)燕子北回，春天來了。
(1)設P：雪是黑色的。Q：2+2>4。則(1)可表示為 ，其真值為T。
(2)設R：燕子北回。S：春天來了。則(2)可表示為
，其真值為T。
與前面的聯結詞一樣，條件聯結詞和雙條件聯結詞連線的兩個命題之間可以沒有任何的因果聯繫，只要能確定複合命題的真值即可。
異或聯結詞
P | Q | P異或Q |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
與非聯結詞
聯結詞“
”的定義如表7所示。
P | Q | P與Q的“與非式” |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
或非聯結詞
定義8 設P、Q為兩個命題公式，複合命題
稱為P和Q的“或非式”。若且唯若P與Q的真值都為F時， 的真值為T，否則 的真值為F。聯結詞“上”的定義如表8所示。
P | Q | P和Q的“或非式” |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
