基本介紹
- 中文名:矛盾式
- 外文名:contradictory formula,unsatisfiable formula
- 別稱:常假式、 永假式、不可滿足式
- 所屬學科:數學(邏輯演算)
基本介紹,相關介紹,
基本介紹
矛盾式亦稱“常假式”、 “永假式”、“不可滿足式”、“真值函項的假命題”。
①命題邏輯中其值常假的真值形式。一個真值形式,若無論其所含命題變元取何值,其值總為假,則該真值形式就是矛盾式。 例如,p∧⌝p、⌝(p∨⌝p)、 p∧⌝(p∨q)等都是矛盾式。 一個真值形式是否為矛盾式,可用真值表判定。 例如, p∧⌝p 的真值表為 (以“T”表示真,以 “F”表示假):
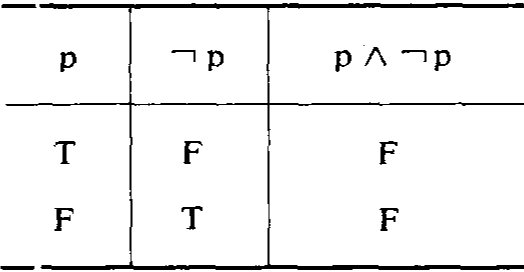 p∧⌝p 的真值表
p∧⌝p 的真值表此表說明,無論命題變元p取何值, p∧⌝p的值總為假, 因此它是一個矛盾式。
②謂詞邏輯中其值常假的公式。一個謂詞邏輯的公式,若無論選擇怎樣的非空個體域,無論用什麼表示特定個 體的詞和表示特定性質或關係的詞分別代替公式中的自由個體變元和謂詞變元,並且無論用什麼具體命題代替公式中的命題變元,其結果總是得到一個假命題,則這個謂詞邏輯的公式就是一個矛盾式。例如,(∃x)(F(x)∧⌝F (x))、(∀x) F(x)∧(∃x)⌝F (x)、(p∧⌝p)∧F(x) 等都是矛盾式。
相關介紹
對於命題公式A,如果對A中命題變元的一切指派,A的真值都為真,則稱命題公式A為重言式,又稱永真式,記作T。
如果對A中命題變元的一切指派,A的真值都為假,則稱命題公式A為矛盾式,又稱永假式,記作F。
如果對A中命題變元的一切指派,A的真值有真有假,則稱A為可滿足式。
那么任何一個公式肯定是永真式、永假式和可滿足式三種公式中的一個,判定一個公式是這三類公式中的哪一個往往稱為公式的判定問題,目前我們可以藉助真值表有效判定。
很顯然,當A是永真式(永假式)時,¬A必為永假式(永真式)。
【例1】對任何公式A,A∨¬A是重言式,A∧¬A是矛盾式。
【例2】下列命題都是矛盾式:
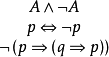
對於矛盾式,也有類似於定理1和定理2的結果。
定理1 任何兩個重言式的析取或合取,仍是一個重言式。
證明 設A、B為兩個重言式,則無論對A與B的分量作何種指派,總有A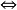 T,B
T,B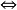 T,故A∨B
T,故A∨B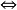 T,A∧B
T,A∧B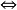 T。
T。
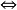
定理2 一個重言式,對同一分量用任何合式公式置換,所得公式仍為一重言式。
證明 因為重言式的真值與分量的指派無關,所以對同一分量用任何合式公式置換後,重言式的真值仍永為真。
例如,P∨¬P為一重言式,用Q∧R置換P。所得新公式(Q∧R)∨¬(Q∧R)仍為重言式。