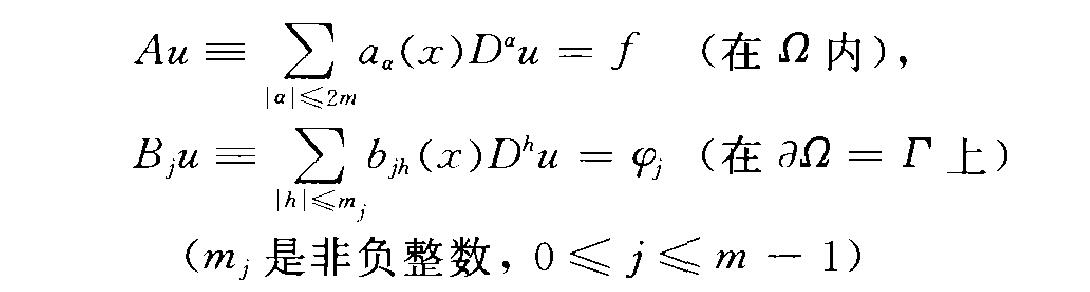
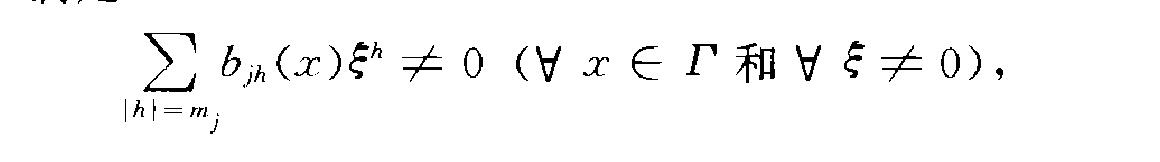

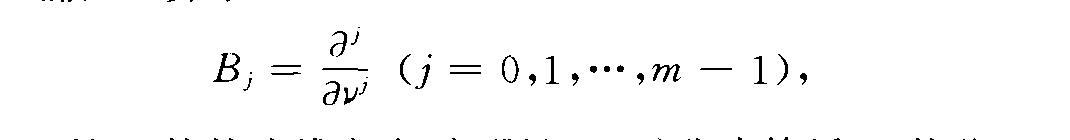
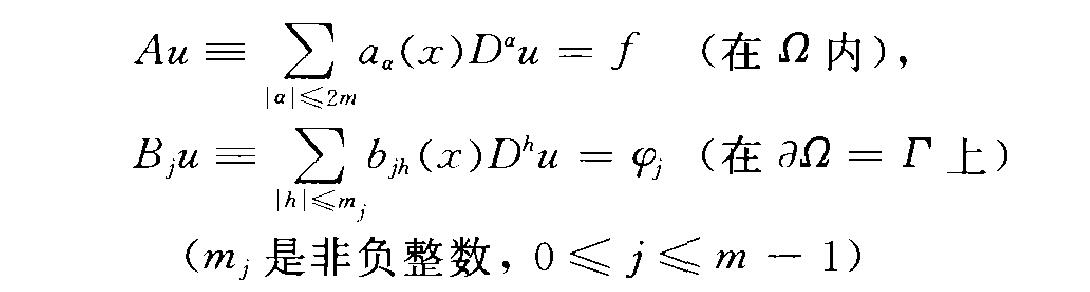
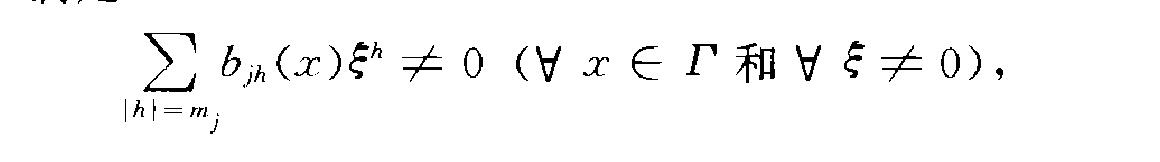

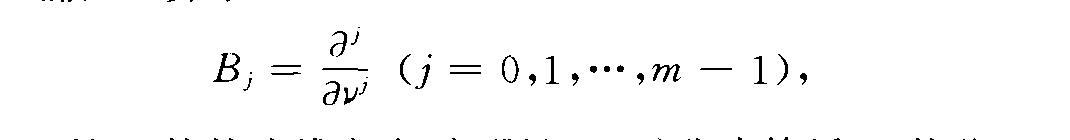
(regular elliptic problem)恰當 橢圓型運算元方程的重要邊值問題.橢圓型方程的邊 值問題 (m,是非負整數,O( j(m一1) 如果滿足下列條件,那么稱它為正則橢圓問題...
伴隨邊值問題是邊值問題中的重要概念。正則橢圓問題由格林公式連結的另一邊值問題。...
4 套用位勢解邊值問題 32 5 Green函式和正則邊界積分方程 36 6 Poisson方程 第二章 數值方法 62 1 邊界單元 62 2 用配置法解間接邊界積分方程 71 3 直接...
混合邊值問題(mixed boundary value prob- lem)典型的非正則橢圓邊值問題.設月是R”中 的有界域,它的邊界r由m個子集r0,r ...,rn,_} 組成.設A是月中的...
來出現的最新技巧,並討論線性方程、擬線性方程以及完全非線性方程 Dirichlet問題的可解性;第H部分介紹線性和非線性橢圓型方程組 Dirichlet問題弱解的存在性和正則性...
(組)定理,橢圓正則化方法,緊微法,變分法等方法,在不動點理論中,最早的結果可算Brouwer不動點定理,即E的閉單位球到自身的連續映射有不動點,這個結果1910年...
內滿足給定的橢圓型方程、在 上取給定的連續邊界值的解的問題,稱為橢圓型方程的狄利克雷問題。特別地,對有界區域 ,如果邊界點都是正則點(參見“閘函式”),調和...
正則化運算元矩陣求逆的正則化 編輯 在某些情況下,為了正確定義機器學習問題, 正則化是必要的。 機器學習中許多線性模型,包括線性回歸和 PCA,都依賴於求逆矩陣 。
的邊界條件稱為斜微商邊界條件,若向量b=(b1,b2,…,bn)的法向分量bν在∂ Ω上非零,則稱上述條件為正則斜微商邊界條件。邊值問題第三邊值問題 編輯 ...
一個復曲面S稱為橢圓曲面,如果存在閉Riemann面 C 與復解析的正則映射π:s — c 為滿射。並且除有限個以外,π的纖維 是非奇異橢圓曲線 (虧格1 的Riemann面)...
斜微商問題是求解滿足斜微商邊界條件的橢圓型方程的解的問題,形如的邊界條件稱為斜微商邊界條件,若向量 的法向分量 在 上非零,則稱上述條件為正則斜微商邊界條件...
2.1.3 邊值問題的正則性估計 2.2 橢圓邊值問題有限元方法 2.2.1 有限元空間 2.2.2 有限元法 ?2.3 橢圓邊值問題有限元法誤差估計 2.3.1 插...
(值域空間)Im.}是閉的並且它的余維數也是有 限的,那么就稱運算元夕是指標運算元.運算元夕的指標 XW)由下式給出:正則橢圓邊值問題{A}B;}對應的運算元是一個指標...
如果令 ε=0,Γε的表達式可化為Γ0,而且是一致有效的,就稱這個攝動問題是正則攝動問題。如果在Sε中令ε=0會導致問題無解或多解,或者雖然當ε=0時Sε能...
其基本思想是:對變數進行一系列適當的正則變換,以求降低運動方程的階次,使新的方程具有較簡單的形式,例如得出一個描述等速直線運動或簡諧振動的方程,從而使問題得...
外爾引理是數學史上關於橢圓正則性的第一個結果。它可以被推廣到一般橢圓運算元的情形。 [1] 外爾引理赫爾曼·外爾 編輯 赫爾曼·克勞斯·胡戈·外爾(Hermann Klaus ...
其基本思想是:對變數進行一系列適當的正則變換,以求降低運動方程的階次,使新的方程具有較簡單的形式,例如得出一個描述等速直線運動或簡諧振動的方程,從而使問題得...
