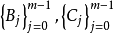伴隨邊值問題是邊值問題中的重要概念。正則橢圓問題由格林公式連結的另一邊值問題。
基本介紹
- 中文名:伴隨邊值問題
- 外文名:adjoint boundary value problem
- 適用範圍:數理科學
邊值問題中的伴隨邊值問題,自伴隨邊值問題,
邊值問題中的伴隨邊值問題
伴隨邊值問題是邊值問題中的重要概念,對於微分式
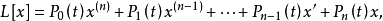

設 為 m* 個邊緣運算元。記
為 m* 個邊緣運算元。記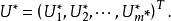 如果對於滿足邊界條件 U[x]=0 的任意的 Cm 類函式 x(t) 和滿足邊界條件
如果對於滿足邊界條件 U[x]=0 的任意的 Cm 類函式 x(t) 和滿足邊界條件 的任意 Cm 類函式 x*(t),有
的任意 Cm 類函式 x*(t),有

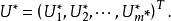

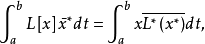


當 L[x]=L*[x] 且條件 U[x]=0 等價於條件 U*[x]=0 時,稱邊值問題是自伴的。
自伴隨邊值問題
正則橢圓問題由格林公式連結的另一邊值問題,在橢圓運算元的格林公式中,邊值問題 {A*,Cj }:

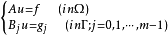
關於格林公式的伴隨邊值問題或者形式伴隨問題,如果 A=A*,格林公式可表為
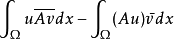

其中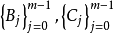 是狄利克雷組,Bj 的階加上 Cj 的階等於 2m-1 。此時問題 {A,Cj} 稱為自伴隨邊值問題,拉普拉斯方程的第一、第二以及第三邊值問題都是自伴隨邊值問題。
是狄利克雷組,Bj 的階加上 Cj 的階等於 2m-1 。此時問題 {A,Cj} 稱為自伴隨邊值問題,拉普拉斯方程的第一、第二以及第三邊值問題都是自伴隨邊值問題。