基本介紹
- 中文名:極小條件
- 外文名:minimal condition
- 所屬學科:數學
- 屬性:有序集相關的一個概念
- 簡介:有序集的任意非空子集都有極小元
基本介紹
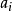
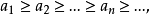
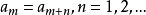
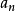
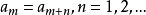
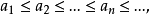
相關定理
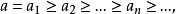
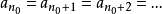
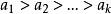
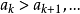
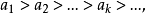
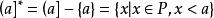
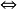
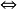
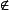

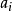
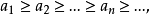
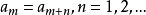
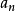
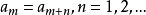
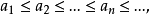
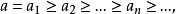
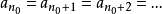
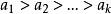
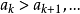
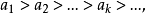
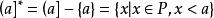
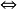
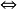
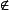
極小條件(minimal condition)是與有序集相關的一個概念,當有序集X的任意非空子集都具有極小元時,稱X滿足極小條件。...
半極小條件是極小條件的推廣。若環 R 的任意真同態像(即同態核不為零)對δ 子環(即具有某種性質的子環)滿足極小條件,則稱 R 對δ 子環有半極小條件。....
條件極大值點與條件極小值點統稱為條件極值點。條件極大值點與條件極小值點的函式值即為函式f(x)在限制條件gj(x)下的條件極值。 [1] ...
在數學中,極小曲面是指平均曲率為零的曲面。舉例來說,滿足某些約束條件的面積最小的曲面。 物理學中,由最小化面積而得到的極小曲面的實例可以是沾了肥皂液後吹...
根據極大極小原理所要求的條件,可以分為拓撲線性空間的極大極小原理,拓撲極大極小原理,數量極大極小原理,拓撲數量極大極小原理等等。根據極大極小原理的形式,...
極小一極大後悔準則(min-max regret criterion ) 不確定型決策準則之一它要求決策最大後悔值儘可能地小.這裡,最大後悔值指不確定條件下某決策可能得到的最壞...
在數學規劃中,對於決策方案的各項限制,常以不等式或方程式的形式出現。在經濟問題中,對目標函式常常要在一定約束條件下求最大值(或最小值),它們包含著用來代表...
若A是正規矩陣則分別是A的極大和極小(根據模數)特徵值)若A是酉矩陣則若 是 矩陣範數而A是下三角矩陣,非奇異(也即 )則:條件數其它條件數 編輯 ...
的歐拉-拉格朗日方程的通解, ,又參數α*和β*使下列邊界條件滿足:則是雅可比方程的兩個線性無關解。如果光滑函式 使泛函在 上取極小(或極大),又設沿 滿足...
s階赫爾德條件連續函式 編輯 函式y=f(x)當自變數x的變化很小時,所引起的因變數y的變化也很小。例如,氣溫隨時間變化,只要時間變化很小,氣溫的變化也是很小的;...
庫恩一塔克爾條件(Kuhn-Tucker condition)判定約束非線性規劃問題的某可行點為極小點的必要條件.對於凸規劃來說,則是判別極小點的充分必要條件.對於約束非線性規劃...
狄里赫利條件屬於傅立葉級數分析使用的條件。傅立葉在提出傅立葉級數時堅持認為...(2)在一個周期內,函式有有限個極大值或極小值。(3) x(t)在單個周期內...
狄利克雷條件是一個信號存在傅立葉變換的充分不必要條件。狄利克雷條件括三方面:(1 )在一周期內,連續或只有有限個第一類間斷點;(2)在一周期內,極大值和極小...
取極小值(或極大值)的必要條件是稱其為勒讓德條件。此外,若沿著場的平穩曲線滿足條件 ,則稱為嚴格勒讓德條件。若則稱為強勒讓德條件。...
外爾斯特拉斯條件是變分積分取強極值的一個必要條件。若y*使泛函 取強極小值,則對所有x∈(x0,x1),q∈R1,外爾斯特拉斯E函式滿足 相應地,對強極大值有 這個...
此式就符合“稻田條件”:1.f(0)=0;2.一階導數大於0,二階導數小於0;3.當L趨於0時,一階導數的極限無窮大(投入的勞動力極少時引起的產出的增加量無窮大);...
鏈條件(chain condition)是可數鏈條件概念的推廣。設κ為任意無窮基數,〈P,≤...則稱a為C的R極大元;若a∈C∧ᗄx∈C(xR-a),則稱a為C的R極小元;若a...
庫恩-塔克爾條件(Kuhn-Tucker condition)是判定約束非線性規劃問題的某可行點為極小點的必要條件。對於凸規劃來說,則是判別極小點的充分必要條件。對於約束非線性...
定理1:(極值存在的必要條件)設 是定義在區域 上的實值函式, , 是 的內點。若 在 處可微,且在 處取得局部極小值.則必有滿足上式的點通常稱為駐點。駐點...
從其幾何圖形可以看出整個馬鞍面沒有極值點,但限制在馬鞍面被平面 平面所截的曲線上,有極小值 1,這個極小值就稱為條件極值。必要條件設在約束條件之下求函式的...
