背景
一般來說,不同的控制作用會使系統沿著不同的途徑(即軌線)運行,但究竟哪一條途徑為最佳,是由目標函式(即性能指標泛函)規定的。因此,不同的目標函式有不同的“最優”含義。而且,對於不同的系統其要求也各不相同。例如在工具機加工中可以要求加工成本最小為最優,在飛彈飛行控制中可以燃料消耗最少為最優,在截擊問題中可選時間最短為最優等。因此,最優指的是使某一選定的性能指標泛函最小為依據的。
最小時間控制系統也稱快速系統,它在飛彈、宇航飛船的姿態控制方面套用很廣泛。如果太空飛行器的姿態受到某種擾動而偏離了給定的平衡狀態,當偏離幅度不超過控制所許可的範圍時,在最短時間內,控制太空飛行器的姿態能恢復到給定的平衡狀態,這就是最小時間控制的概念。最小時間控制又是極小值原理套用的範例。
極小值原理
極小值原理(minimum principle)估計超調和函式極小值點的位置的論斷,為位勢論的基本原理之一若f在區域D (DCR")內超調和。
其中∂D是D在R-=R∪{∞}中的邊界;若f在某個x0∈D達到極小值,則f≡f(x0).特別地,D內調和函式若非常數不能在內點達到極小值.這些性質分別稱為超調和函式與調和函式的極小值原理.類似地,對於下調和函式與調和函式,有極大值原理。
定義
能以最短時間完成規定控制作用的
最優控制系統,又稱快速控制系統。例如,太空飛行器的姿態由於擾動而偏離給定的平衡狀態,在快速控制系統的作用下,即能在最短的時間內恢復到原平衡狀態。
60年代末,對於線性定常的被控對象,最速控制系統的設計問題已基本解決。在這類快速控制問題中,受控對象是線性定常系統,其狀態方程(見
狀態空間法)為
x(0)=x0
式中x(t)是狀態向量,u(t)是控制向量,A和B是由系統結構和參數所決定的係數矩陣。控制向量u(t)的各個分量u1,u2,…,um的幅值只能在容許範圍內取值,這一約束條件可表示為:
|ui|≤Mi (Mi為一正常數,i=1,2,…,m)
設計的目的是確定最優控制向量u*(t)(0≤t≤τ),使被控對象在u*(t)的作用下能夠用最短的時間τ由初始狀態x0轉移到指定的終點狀態x(τ)=0。
套用
極大值原理可以很好地解決線性定常受控對象的快速控制問題。其結論是:①若受控對象能控(見
能控性),則最優控制向量u*(t)唯一地存在。②u*(t)是個
開關函式,每個分量u壟(i=1,2,…,m)都分段取常值+Mi或-Mi。③如果A的特徵根均是實數,則u壟值在+M和-M之間切換的次數不大於n-1,n為特徵根數。④u*(t)可表示為狀態變數x(t)的非線性函式,這一函式關係可用計算機來實現。對於一般情況的最速控制問題並無普遍適用的結果。
問題的提出
最短時間控制問題又稱快速控制問題。尋找一個最優控制,使系統由初始狀態轉移到指定的目標集(即終端狀態),且所用的時間最少,即為快速控制所要解決的問題。下面以雙積分系統為例研究最短時間控制問題。
二階系統的最簡單情形即為雙積分系統,其狀態方程可表示為
設U受到不等式約束,即
初始時刻t
0=0;初始狀態為
,
;終端狀態為
,
。性能指標為
尋求最優控制,使狀態從x(o)轉移到
,且使J取最小值。
用最小值原理求解。寫出哈密頓函式:
求得協態方程為
因此為一條直線。其可能的形式如圖所示。
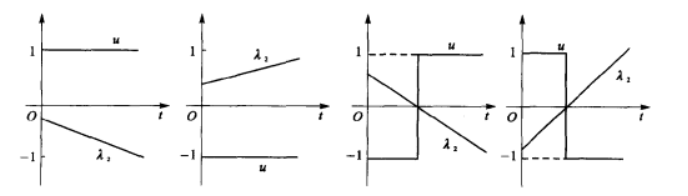 u的變化規律
u的變化規律只在孤立的時刻有
,根據條件,在最優解時,為使H最小,可判定u應滿足下面的
表示了u的取值條件及規律。在整個控制過程中,在一1,十1之間最多只有一次轉換,因此最優控制規律只有以下四種可能的方式:
為確定究竟選哪一種控制方式,在不同初值時,上述方程在平面上為兩簇拋物線,如圖所示。
其中只有兩半支曲線終止於坐標原點,如圖所示。
由此可見,起始於狀態平面上任一點的運動要想到達坐標原點,必須先轉移到y+或y-曲線上,再取u=+1或u=-1的控制,使狀態沿y+或y-趨向原點,因此初始狀態位於y+,y-曲線上方開始的運動,必先取u=-1的控制,使狀態轉移到y+上,然後將控制轉換為u=+1即可用最短時間將狀態轉移到原點。
綜上所述,可將雙積分系統的最優控制規律表述如下:
上述控制過程可由下圖的結構實現口確定控制規律之後,利用狀態方程可求得控制過程所用的最短時間。
時間控制定義
按照預定的時間間隔依次控制電動機起動或制動的方法。例如,在一定的時間範圍內,依次分段切除起動電阻,實現電動機自動起動。通常由時間繼電器在來實現。每隔一定時間,由時間繼電器發出指令,使加速接觸器動作,依次切除加速(或制動)電阻,使電動機加速(或制動)。廣泛用於起重機及船舶機械電力拖動中。
數學基礎
狀態空間法的主要數學基礎是線性代數。在狀態空間法中,廣泛用向量來表示系統的各種變數組,其中包括
狀態向量、輸入向量和輸出向量。變數的個數規定為相應向量的
維數。用x表示系統的狀態向量,用u和y分別表示系統的輸入向量和輸出向量,則系統的
狀態方程和量測方程可表示為如下的一般形式:
x'=f(x,u,t), y=g(x,u,t)
式中,f(x,u,t)和g(x,u,t)為
自變數x、u、t的非線性向量函式,t為時間變數。對於
線性定常系統狀態方程和量測方程具有較為簡單的形式:
x'=Ax+Bu, y=Cx+Du
式中A為系統矩陣,B為輸入矩陣,C為輸出矩陣,D為直接傳遞矩陣,它們是由系統的結構和參數所定出的常數矩陣。在狀態空間法中,控制系統的分析問題常歸結為求解系統的
狀態方程和研究狀態方程解的性質。這種分析是在
狀態空間中進行的。所謂狀態空間就是以
狀態變數為
坐標軸所構成的一個
多維空間。
狀態向量隨時間的變化在狀態空間中形成一條軌跡。對於
線性定常系統,狀態軌跡主要由系統的
特徵值決定。系統的特徵值規定為系統矩陣A的
特徵方程det(sI-A)=0的根,其特徵可由它在s
複數平面上的分布來表征。當運用狀態空間法來綜合控制系統時,問題就變為選擇一個合適的輸入
向量,使得狀態軌跡滿足指定的性能要求。
優點
狀態空間法有很多優點。由於採用矩陣表示,當
狀態變數、輸入變數或輸出變數的數目增加時,並不增加系統描述的複雜性。狀態空間法是
時間域方法,所以很適合於用
數字電子計算機來計算。狀態空間法能揭示系統內部變數和
外部變數間的關係,因而有可能找出過去未被認識的系統的許多重要特性,其中
能控性和
能觀測性尤其具有特別重要的意義。研究表明,從系統的結構角度來看,狀態變數描述比
經典控制理論中廣為套用的輸入輸出描述(如
傳遞函式)更為全面。
意義
控制模式和數學模型
當水輪發電機組投入大電網中並列運行時,機組輸出功率的變化不影響機組頻率,在這種運行狀態下,調速器變成開環系統,按照人為的負荷整定值來調節水輪機導葉開度,其示意圖如圖1所示,這時調速器成為一個隨動調節裝置。
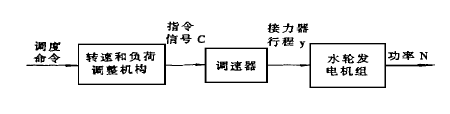 圖1機組負荷調整示意圖
圖1機組負荷調整示意圖當調速器作為隨動調速工作時,其調節作用具有滯後性,顯著提高調節的速動性可採用機組切除緩衝器的運行方式,這在機組並列於大容量電網中運行,而機組容量所占比重不大時是適宜的。事實上,在實用的最短時間控制中,一般均是採用雙重反饋模型結構的,即以快速最優過程消除大幅度偏差,以常規的方式消除小偏惹這樣可以避免在最短時間控制過程中出現的極限環,有利於提高控制系統的穩定性,只需在偏差小於允許誤差時,由開關控制切換至常規的PID(或PI)控制即可因此,在對機組進行負荷調整時,可先切除暫態反饋,以快速最優過程消除大幅度偏差,當偏差小於某個允許誤差時,再投入暫態反饋進行PID(或PI)調故在一定水頭下,當機組穩定時,由(2)式可知,水輪機導葉開度與水輪機的轉矩是一一對應的,而轉矩乘角速度等於功率,角速度可通過系統頻率計算求出。這樣就可以把機組負荷調整的最短時間控制轉化成對應的水輪機導葉開度調整的最短時間控制。也就是說,當需要把機組的負荷P調整到P0時,可根據系統頻率計算出對應於P0的水輪機轉矩mt0,由mt0和當時的水頭h。












 u的變化規律
u的變化規律



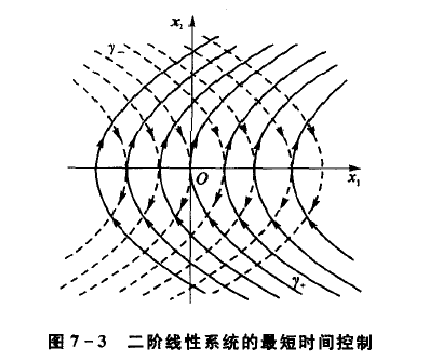
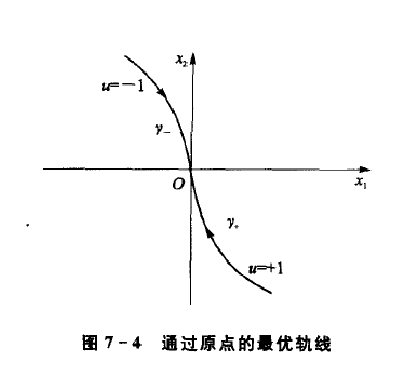


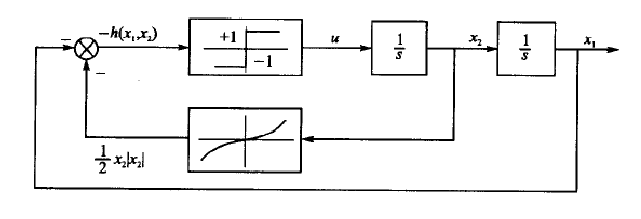
 圖1機組負荷調整示意圖
圖1機組負荷調整示意圖