數學上,施瓦茲引理是複分析關於定義在單位開圓盤的全純函式的一個結果,以赫爾曼·阿曼杜斯·施瓦茨為名。
基本介紹
- 中文名:施瓦茲引理
- 外文名:Schwarz lemma
- 分類:數理科學
- 套用範圍:數學定理
簡介


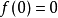
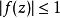
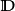


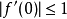
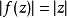
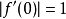
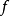


證明

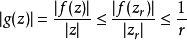

施瓦茲—皮克定理

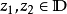



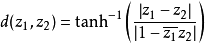
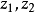
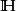

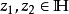
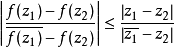

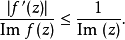
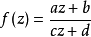

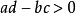
數學上,施瓦茲引理是複分析關於定義在單位開圓盤的全純函式的一個結果,以赫爾曼·阿曼杜斯·施瓦茨為名。


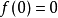
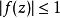
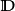


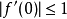
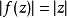
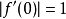
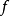



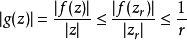


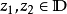



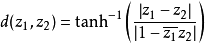
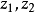
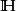

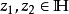
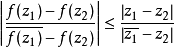

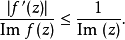
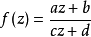

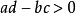
數學上,施瓦茲引理是複分析關於定義在單位開圓盤的全純函式的一個結果,以赫爾曼·阿曼杜斯·施瓦茨為名。...
施瓦茨引理是複分析關於定義在單位開圓盤的全純函式的一個結果,以赫爾曼·阿曼杜斯·施瓦茨為名。...
廣義施瓦茲引理(generalized Schwarz's lemma )是施瓦茲引理的推廣。...... 廣義施瓦茲引理(generalized Schwarz's lemma )是施瓦茲引理的推廣。概念若f (z)在}z}<...
定理概述施瓦茨引理有一個版本是在單位圓盤的解析自同構(即單位圓盤 的全純雙射)下不變。這稱為施瓦茨—皮克定理。 設<math>f:\Delta\to\Delta</math> 全純...
以他為名的有柯西-施瓦茨不等式、施瓦茨導數、施瓦茨-克里斯托費爾映射、施瓦茨反射原理和施瓦茨引理。詞條標籤: 科學家 , 數學家 , 人物 ...
嘉當惟一性定理是單複變函數論中施瓦茲引理的推廣。嘉當(Cartan,H.)把施瓦茲引理推廣到多複變函數,得到所謂的嘉當惟一性定理。...
皮克的不變形式的施瓦茲引理敘述如下:映單位圓入自身的解析映射使得兩點間的雙曲距離,曲線的雙曲長度和集合的雙曲測度縮小,僅當映射是上述麥比烏斯變換時,這些量...
3 亞橢圓常係數微分運算元 4 施瓦茲定理 5 定強微分運算元 常係數微分運算元基本介紹...引理1 設 具定強,對固定的 令 並設 是弱於 的常係數運算元的有限維向量空間...
關於極小集的結構,施瓦茲(A.J.Schwarz)於1963年將上述結果推廣到定義於二維流形上的C2類流,得到下述結論(亦稱施瓦茲定理):C2類流形M上的C2流的非空緊極小集...
