廣義施瓦茲引理

概念

廣義施瓦茲引理是施瓦茲引理的推廣。

若f(z)在|z|<1內解析，且|f(z)|<1，則對於|z|<1內任意兩點z₁,z₂，有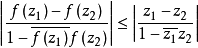

及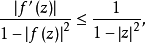

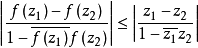
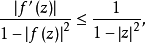
其中，等號僅當f(z)為分式線性變換時成立。

設

為複平面中的開圓盤，如果

1.

是全純函式；

2.

；

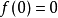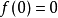
3.

。

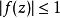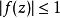
那么對所有在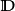

中的

，

成立，且

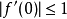。如果等式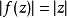

對某個不為0的z₀成立，或

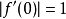，那么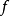

是一個旋轉：

，其中

。

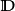
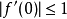
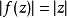
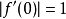
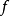
這引理不及其他結果有名（例如黎曼映射定理，其證明有用到這引理），但卻是能顯示全純函式的嚴格性的一個簡單結果。對於實函式則沒有類似的結果。

給定滿足條件ad-bc≠0的四個復常數a，b，c，d，把由函式w=f(z)=(az+b)/(cz+d)定義的變換稱為分式線性變換，定義中的條件ad-bc≠0 是為了保證變換的保角性。

分式線性變換是最簡單的共形映射，同時也是共形映射一般理論的基礎，並且具有許多幾何直觀十分明顯的重要性質。在建立邊界為圓弧或直線的區域之間的共形映射時，分式線性變換是一個非常有利的工具。