斜微商問題(oblique derivative problem)是求解滿足斜微商邊界條件的橢圓型方程的解的問題,又稱諾伊曼邊值問題、第二邊值問題,它的邊界條件是給出未知函式關於區域邊界的法嚮導數或非切嚮導數。
基本介紹
- 中文名:斜微商問題
- 外文名:oblique derivative problem
- 所屬學科:數學
- 別名:諾伊曼邊值問題、第二邊值問題
- 所屬問題:偏微分方程(偏微分方程基本解法)
- 相關概念:斜微商邊界條件、橢圓型方程等
簡介




唯一性定理








問題分析




























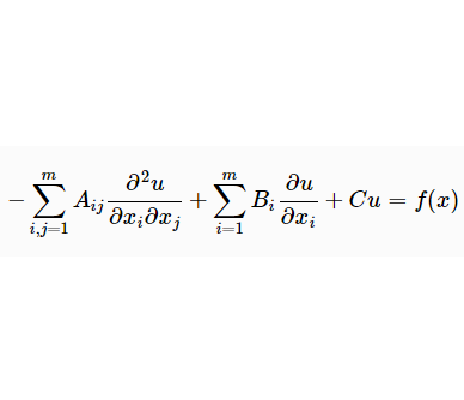
斜微商問題(oblique derivative problem)是求解滿足斜微商邊界條件的橢圓型方程的解的問題,又稱諾伊曼邊值問題、第二邊值問題,它的邊界條件是給出未知函式關於區域邊界的法嚮導數或非切嚮導數。








































斜微商問題(oblique derivative problem)是求解滿足斜微商邊界條件的橢圓型方程的解的問題,又稱諾伊曼邊值問題、第二邊值問題,它的邊界條件是給出未知函式關於區域邊界的法嚮導數或非切嚮導數。簡介斜微商...
斜微商邊界條件 斜微商邊界條件是一個數學術語。斜微商邊界條件(oblique derivative boundarycondition)見“斜微商問題,,.
正則斜微商邊界條件 正則斜微商邊界條件,正則斜微商邊界條件(regular oblique deriva-tive boundary condition)見“斜微商問題”.
邊值問題是定解問題之一。只有邊界條件的定解問題稱為邊值問題。二階偏微分方程(組)一般有三種邊值問題:第一邊值問題又稱狄利克雷問題,它的邊界條件是給出未知函式本身在邊界上的值;第二邊值問題又稱諾伊曼邊值問題或斜微商問題...
對於同樣的Neumann問題,通過另外兩種完全不同的方法,建立了其全局的梯度估計。研究形式較為一般的增廣Hessian方程的斜微商問題,在矩陣A滿足A3w條件時,討論了方程的線性和非線性斜微商問題的全局二階導數估計,進而得到了經典解的存在性...
討論了半球面上的質量傳輸問題,得到了Monge問題解的存在性和唯一性的充分條件。分別研究了最優傳輸問題所對應的Monge-Ampere型方程、Hessian方程的Dirichlet問題、斜微商問題,給出了解的直到二階導數的先驗估計,達到了經典解的存在性和唯一...
(2)利用所研究的奇異積分運算元給出了一些邊值問題的積分表示,例如:Cimmino方程組的一類混合邊值問題、加權Dirac運算元的Riemann邊值問題、退化的橢圓方程組的Riemann邊值問題和斜微商邊值問題以及與Helmholtz方程有關的邊值問題等;(3)...
目標在於研究這類方程的各類邊值問題(如Dirichlet邊值和斜微商邊值問題等)的可解性,對求解區域尋找合適的幾何條件,以保證邊值問題解的存在性和正則性;對方程中的參數趨近於其臨界情形時,我們研究問題解的漸近行為,以加深對其幾何...
特別是在平面凹多邊形中,最好的模型——Laplace方程在凹性角點附近無論是Dirichlet邊值條件、Neumann邊值條件、Robin邊值條件、正則斜微商條件還是混合邊值條件中,哪一種邊值條件最好也就是解具有Holder連續性,這說明“非光滑”的困難...
以及二階雙曲型複方程的的斜微商問題,給出了這些問題的可解性結果;提出並論證了多連通區域上帶Riemann-Hilbert型映射的橢圓型複方程係數反演問題,給出了重構係數的一種新方法,同時證明了這一反問題解的整體唯一性。
這種二階混合型方程包含空氣動力學中著名的Chaplygin 方程作為特殊情況,而邊值問題包括Tricomi 問題,Frankl問題和斜微商問題等. 第七章主要介紹上述理論和方法在非線性力學邊值問題中的套用。
弱解理論導論; 赫爾德估計; 解的存在性、惟一性和解的正則性;再論弱解理論;強解;定點定理及其套用;比較原理和極大值原理;邊界梯度估計; 全局和局部梯度邊界;赫爾德梯度估計和存在性定理; 擬線性拋物方程用的斜微商問題;一般非線性...
求解問題 假設在變數 的 維空間的某一區城D, 和 為其變數 的可微函式。已給變數 的任一函式,若此函式對這些變數都有偏導數,且能使方程(2)化為恆等式,則稱此函式為方程(2)的解。和線性方程一樣,可以把此解解釋為...
