斐波那契(斐波那契，L.)

斐波那契

斐波那契，L.一般指本詞條

斐波那契（Leonardo Pisano ,Fibonacci, Leonardo Bigollo，1175年-1250年），中世紀義大利數學家，是西方第一個研究斐波那契數的人，並將現代書寫數和乘數的位值表示法系統引入歐洲。其寫於1202年的著作《計算之書》中包含了許多希臘、埃及、阿拉伯、印度、甚至是中國數學相關內容。

基本介紹

  • 中文名：斐波那契
  • 外文名：Leonardo Pisano, Fibonacci, Leonardo Bigollo
  • 國籍：義大利
  • 出生日期：1175年
  • 逝世日期：1250年
  • 職業：數學家
  • 主要成就：斐波那契數列
  • 代表作品：《算盤全書》、《計算之書》
  • 父親：Guilielmo（威廉）
人物背景,家庭,學習,成就,人物軼事,數列,質數,C計算代碼,重要作品,

人物背景

家庭

李奧納多的父親名為Guilielmo（威廉），外號Bonacci（意即「好、自然」或「簡單」）。威廉是商人，在北非一帶工作（今阿爾及利亞Bejaia），當時年輕的李奧納多已經開始協助父親工作，他學會了阿拉伯數字。

學習

有感使用阿拉伯數字比羅馬數字更有效，李奧納多前往地中海一帶向當時著名的阿拉伯數學家學習，約於1200年回國。1202年，27歲的他將其所學寫進《計算之書》（Liber Abaci）。這本書通過在記賬、重量計算、利息、匯率和其他的套用，顯示了新的數字系統的實用價值。這本書大大影響了歐洲人的思想，可是在三世紀後印製術發明之前，十進制數字並不流行。（例子：1482年，Ptolemaeus世界地圖 ，Lienhart Holle在Ulm印製）

成就

李奧納多曾成為熱愛數學和科學的腓特烈二世(神聖羅馬帝國的皇帝)的座上客。
歐洲數學在希臘文明衰落之後長期處於停滯狀態，直到12世紀才有復甦的跡象。這種復甦開始是受了翻譯、傳播希臘、阿拉伯著作的刺激。對希臘與東方古典數學成就的發掘、探討，最終導致了文藝復興時期（15～16世紀）歐洲數學的高漲。文藝復興的前哨義大利，由於其特殊地理位置與貿易聯繫而成為東西方文化的熔爐。義大利學者早在12～13世紀就開始翻譯、介紹希臘與阿拉伯的數學文獻。
在歐洲，黑暗時代以後第一位有影響的數學家斐波那契（約1175年～1250年），其拉丁文代表著作《計算之書》（Liber Abaci）和《幾何實踐》（Practica Geometriae）也是根據阿拉伯文與希臘文材料編譯而成的，斐波那契即比薩的李奧納多（Leonardo of Pisa），早年隨父在北非從師阿拉伯人習算，後又遊歷地中海沿岸諸國，回義大利後即寫成《計算之書》（Liber Abaci，1202，亦譯作《算盤算經》）。《計算之書》最大的功績是系統介紹印度記數法，影響並改變了歐洲數學的面貌。現傳《算經》是1228年的修訂版，其中還引進了著名的“斐波那契數列”。《幾何實踐》（Practica Geometriae， 1220）則著重敘述希臘幾何與三角術。
斐波那契其他數學著作還有《平方數書》（Liber Quadratorum，1225）、《花朵》（Flos，1225）等，前者專論二次丟番圖方程，後者內容多為腓特烈二世（Frederick II）宮廷數學競賽問題，其中包含一個三次方程/十2x2十10x～－20求解，斐波那契論證其根不能用尺規作出（即不可能是歐幾里得的無理量），他還未加說明地給出了該方程的近似解（J一1.36880810785）。
微積分的創立與解析幾何的發明標誌著文藝復興後歐洲近代數學的興起。微積分的思想根源部分（尤其是積分學）可以追溯到古代希臘、中國和印度人的著作。在牛頓和萊布尼茨最終制定微積分以前，又經過了近一個世紀的醞釀。在這個醞釀時期對微積分有直接貢獻的先驅者包括克卜勒、卡瓦列里、費馬、笛卡爾、沃利斯和巴羅（1．Barrow，1630年～1677年）等一大批數學家。

人物軼事

數列

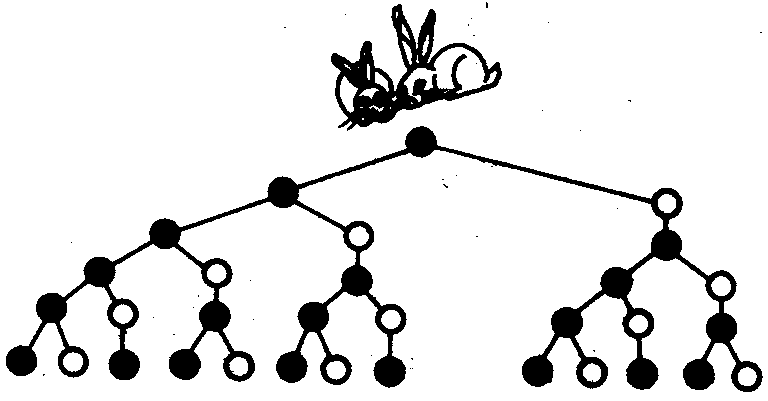
斐波那契在《計算之書》中提出了一個有趣的兔子問題：
斐波那契(斐波那契，L.)
兔子問題
一般而言，兔子在出生兩個月後，就有繁殖能力，一對兔子每個月能生出一對小兔子來。如果所有的兔子都不死，那么一年以後可以繁殖多少對兔子？
我們不妨拿新出生的一對小兔子分析一下：
第一個月小兔子沒有繁殖能力，所以還是一對；
兩個月後，生下一對小兔總數共有兩對；
三個月以後，老兔子又生下一對，因為小兔子還沒有繁殖能力，所以一共是三對；
……
依次類推可以列出下表：
經過月數
0
1
2
3
4
5
6
7
8
9
10
11
12
總體對數
0
1
1
2
3
5
8
13
21
34
55
89
144
表中數字1，1，2，3，5，8－－－構成了一個序列。這個數列有關十分明顯的特點，那是：前面相鄰兩項之和，構成了後一項。這個數列是義大利中世紀數學家斐波那契在《計算之書》中提出的，這個級數的通項公式，除了具有an+2=an+an+1的性質外，還可以證明通項公式為：an=1/√5 [（1/2+√5/2）^ n-（1/2-√5/2）^n](n=1,2,3.....)（√5表示根號 5）。
斐波那契(斐波那契，L.)
兔子問題
這個通項公式中雖然所有的an都是正整數，可是它們卻是由一些無理數表示出來的。
即在較高的序列，兩個連續的“斐波納契數”的序列相互分割將接近黃金比例（1.618:1或1:0.618）。
例如：233/144，987/610……
斐波那契數列還有兩個有趣的性質：
⒈斐波那契數列中任一項的平方數都等於跟它相鄰的前後兩項的乘積加1或減1；
斐波那契(斐波那契，L.)
兔子問題
⒉任取相鄰的四個斐波那契數，中間兩數之積（內積）與兩邊兩數之積（外積）相差1。

質數

斐波那契質數由斐波那契序列中的質數組成，是整數質數序列。
第一組質數序列是：2，3，5，13，89，233，1597，28657，514229，433494437，2971215073……

C計算代碼

1.
#include <stdio.h>
int fib(int x)
{
    if(x==1 || x==2)
    {
        return 1;
    }
    else
    {
        return fib(x-1)+fib(x-2);
    }
}
int main()
{
    int n=0;
    scanf("%d",&n);
    printf("%d",fib(n));
}
2.
#include <stdio.h>
int fib[1000001]={0,1,1};
int main()
{
    int n=0;
    scanf("%d",&n);
    for(int i=3;i<=n;i++)
    {
        fib[i]=fib[i-1]+fib[i-2];
    }
    printf("%d",fib[n]);
    return 0;
}

重要作品

Liber Abaci（計算之書，1202年）。
Practica Geometriae（幾何實踐，1220年）。
Flos（花朵，1225年），Johannes of Palermo提出的問題的答案。
Liber quadratorum（平方數書）關於丟番圖方程的問題on Diophantine problems,that is,problems involving Diophantine equations.
Di minor guisa（關於商業運算；已佚）
《幾何原本》第十卷的注釋（已佚）
拉丁文代表著作《珠算原理》

相關詞條

熱門詞條

聯絡我們