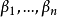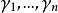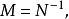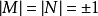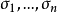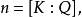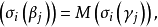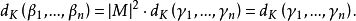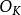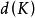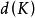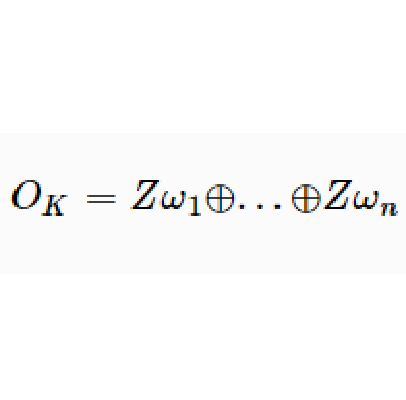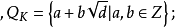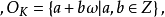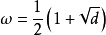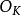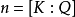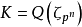基本介紹
- 中文名:整基
- 外文名:integral basis
- 所屬學科:數學
- 所屬領域:數論(代數數論)
- 相關概念:整數環、數域、相對整基等
定義,相關概念與性質,定義1,定理1,定理2,定理3,數域的判別式,
定義
設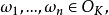 如果
如果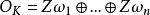 ,則稱
,則稱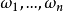 是整數環
是整數環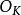 或者數域K的一組整基,換句話說,
或者數域K的一組整基,換句話說,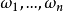 是K或
是K或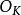 的一組整基,若且唯若每個整數
的一組整基,若且唯若每個整數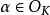 均可唯一地表示成
均可唯一地表示成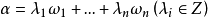 。
。
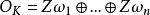
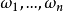
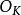
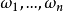
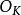
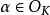
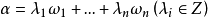
相關概念與性質
定義1
群G叫作是秩為n 的自由Abel群,如果它同構於n 個有理整數加法群Z的直和: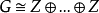 (n個)。換句話說,即存在G中n 個元素
(n個)。換句話說,即存在G中n 個元素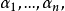 使得G中每個元素均可唯一地表示成
使得G中每個元素均可唯一地表示成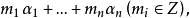 這可以寫成
這可以寫成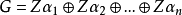 。注意零群(0) 看成是秩為0 的自由Abel 群。
。注意零群(0) 看成是秩為0 的自由Abel 群。
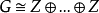
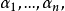
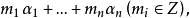
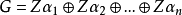
定理1
定理2
定理3
數域的判別式
定理2表明每個數域均存在整基,但是並不是唯一的,例如由定理1可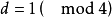 知,對於: 二次域
知,對於: 二次域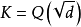 (
(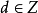 ,無平方因子),當
,無平方因子),當 時,
時,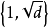 是域K的整基;而當時,
是域K的整基;而當時,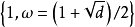 是域K的整基。另一方面,如果我們令
是域K的整基。另一方面,如果我們令
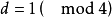
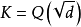
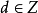

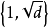
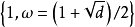
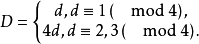
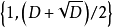
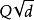
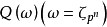
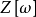
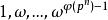
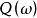
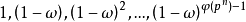
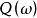
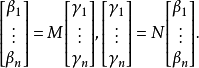
假設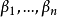 和
和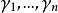 均是數域K的整基,從整基的定義可知存在元素屬於Z的兩個非異方陣M和N,使得
均是數域K的整基,從整基的定義可知存在元素屬於Z的兩個非異方陣M和N,使得