擴展的實數軸

擴展的實數軸由實數軸加上“+∞”和“−∞”得到（注意“+∞”和“−∞”並不是實數），寫作或 [−∞,+∞]。擴展的實數軸在研究數學分析，特別是積分時非常有用。

基本介紹

• 中文名：擴展的實數軸
• 外文名：無
• 目的：數學分析
• 學科：數學

擴展

對任意實數a，定義 −∞ ≤a≤ +∞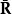，就成了一個全序集。這種集合有種非常好的性質，就是其所有子集都有上確界和下確界：這是一個完備格。全序關係在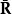上引入了拓撲。在這個拓撲中，集合U是 +∞ 的鄰域，若且唯若它包含集合 {x|x≥a}，這裡a是某個實數。−∞ 的鄰域類似。 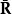是個緊緻的豪斯多夫空間，與單位區間 [0,1] 同胚。

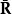
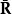
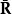
R上的算術運算可以部分地擴展到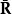，如下：

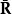
• 若a ≠ −∞，則a + ∞ = ∞ + a = ∞
  
• 若 a ≠ +∞，則a − ∞ = −∞ + a = −∞
  
• 若a > 0，則a × +∞ = +∞ ×a = +∞
  
• 若a < 0，則a × +∞ = +∞ ×a = −∞
  
• 若 a > 0，則a × −∞ = −∞ × a = −∞
  
• 若 a < 0，則a × −∞ = −∞ × a = +∞
  
• 若 −∞ < a < +∞，則a ÷±∞ = 0
  
• 若 0 < a < +∞，則±∞ ÷ a = ±∞
  
• 若 −∞ < a < 0，則+∞ ÷ a = −∞
  
• 若 −∞ < a < 0，則−∞ ÷ a = +∞
  

通常，不定義 ∞ − ∞，0 × ±∞ 和 ±∞ ÷ ±∞。同時，1 ÷ 0 也不定義為 +∞ （因為無足夠強的理由說明為何不定義為 −∞ ）。這些規則是根據無窮極限的性質確定的。

注意，在這些定義下， 不是域，也不是環。

性質

經過上述定義，擴展的實數軸仍有很多實數的性質：

• a + (b + c) 和 (a + b) +c 相等或同時沒有定義。
  
• a + b 和b + a 相等或同時沒有定義。
  
• a(bc) 和(ab)c 相等或同時沒有定義。
  
• ab 和ba相等或同時沒有定義。
  
• a(b + c) 和 ab +ac 若都有定義則相等。
  
• 若 a ≤ b 且 a + c 和b +c 都有定義，則a +c ≤ b +c。
  
• 若a ≤ b 且 c > 0 且ac 和 bc 都有定義，則 ac ≤ bc。
  

通常，只要表達式都有定義，R的算術性質在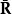上也成立。

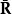
按照極限，一些函式可以自然地擴展到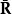。例如，可以定義exp(−∞) = 0，exp(+∞) = +∞，ln0 = −∞，ln(+∞) = +∞ 等等。