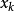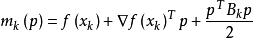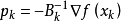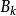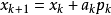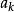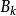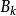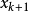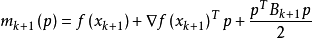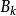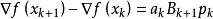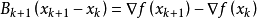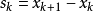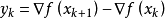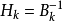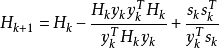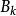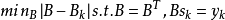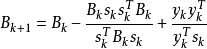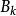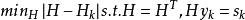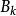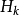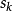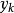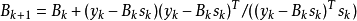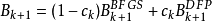擬牛頓法(Quasi-Newton Methods)是求解非線性最佳化問題最有效的方法之一，於20世紀50年代由美國Argonne國家實驗室的物理學家W. C. Davidon所提出來。
Davidon設計的這種算法在當時看來是非線性最佳化領域最具創造性的發明之一。不久R. Fletcher和M. J. D. Powell證實了這種新的算法遠比其他方法快速和可靠，使得非線性最佳化這門學科在一夜之間突飛猛進。在之後的20年裡，擬牛頓方法得到了蓬勃發展，出現了大量的變形公式以及數以百計的相關論文。
基本介紹
- 中文名：擬牛頓法
- 外文名：Quasi-Newton Methods
- 年代：50年代
- 世紀：20世紀
- 類別：物理力學
- 提出者：W. C. Davidon
基本概念,基本思想,DFP方法,BFGS方法,對稱秩1（SR1）方法,Broyden族,
基本概念
擬牛頓法和最速下降法(Steepest Descent Methods)一樣只要求每一步疊代時知道目標函式的梯度。通過測量梯度的變化，構造一個目標函式的模型使之足以產生超線性收斂性。這類方法大大優於最速下降法，尤其對於困難的問題。另外，因為擬牛頓法不需要二階導數的信息，所以有時比牛頓法(Newton's Method)更為有效。如今，最佳化軟體中包含了大量的擬牛頓算法用來解決無約束，約束，和大規模的最佳化問題。
擬牛頓法是解非線性方程組及最最佳化計算中最有效的方法之一.它是一類使每步疊代計算量少而又保持超線性收斂的牛頓型疊代法。
擬牛頓法還有很多具體算法，這類算法最早是由戴維登(Davidon，W.D.)於1959年提出的，弗萊徹(Fletcher，R.)和鮑威爾(Powell，M.J.D.)於1963年給出了後來稱為DFP的秩2擬牛頓法，布羅依丹(Broyden，C.G.)於1965年給出了秩1擬牛頓法.方法的收斂性是20世紀60年代末到20世紀70年代才逐漸被證明的.由於這類方法受到廣泛注意，從20世紀60年代到20世紀70年代近20年中，前後發表了一千多篇文章，提出了很多不同的算法及收斂性證明。中國也有一些學者在這方面做出很好的結果。
基本思想
擬牛頓法的基本思想如下。首先構造目標函式在當前疊代
的二次模型：
我們儘可能地利用上一步的信息來選取 。具體地，我們要求
，從而得到
DFP方法
記
，
，
，DFP公式為
該公式最初由Davidon於1959年提出，隨後被Fletcher和Powell研究和推廣。DFP方法是秩-2更新的一種，由它產生的矩陣
是正定的，而且滿足這樣的極小性：
BFGS方法
DFP更新公式非常有效，但很快就被BFGS公式取代。BFGS與DFP十分類似，是另一種秩-2更新，以其發明者Broyden, Fletcher, Goldfarb和Shanno的姓氏首字母命名。BFGS公式為
由他產生的矩陣 同樣保持正定性，而且也滿足一個極小性：
BFGS和DFP公式在形式上是對稱的： 與
對稱，
與
對稱。但是BFGS比DFP更加有效。
對稱秩1（SR1）方法
有別於DFP和BFG方法，SR1是一種秩-1更新。它的公式是：
。SR1公式不要求矩陣B_k保持正定性，從而更逼近真實的Hesse矩陣，所以適用於信賴域方法(Trust Region Methods)。
Broyden族
Boyden族是更廣泛的一類更新公式，其形式為：
。當
時，Broyden族公式就變成了BFGS公式；當
時，Broyden族公式就變成了DFP公式。因此BFGS和DFP均可看成Broyden族的特殊形式或者其中一員。
