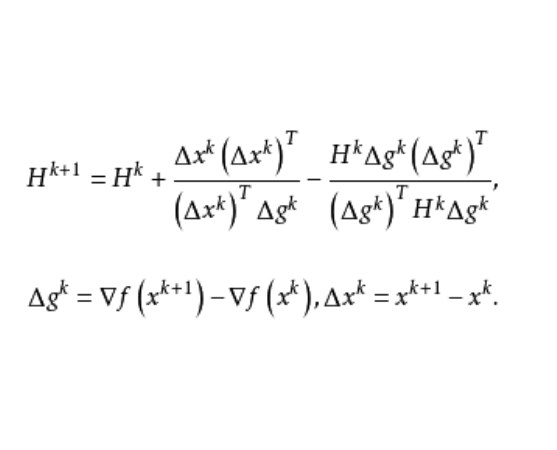尺度矩陣

尺度矩陣(metric matrix)是擬牛頓法修正公式中的矩陣，在求解無約束多變數函式極值的變尺度法(或稱擬牛頓法)中，用尺度矩陣A^k代替了牛頓法的漢森矩陣逆矩陣，從而使牛頓法變得簡單、實用。構成尺度矩陣不需要求取目標函式的二階導數，只需要求其一階導數▽f(x)，構造尺度矩陣時，必須滿足下列擬牛頓條件：A^kΔgⁱ=Δxⁱ，i<k，i≠k；Δgⁱ=▽f(xⁱ⁺¹)-▽f(xⁱ)；Δxⁱ=xⁱ⁺¹-xⁱ。對於n維正定二次函式f(x)，初始的尺度矩陣(A)可選用單位矩陣(I)，給定初始點x¹，令搜尋方向為P¹=-I×▽f(x₁)，並求出此方向上的極值點x²，根據向量共軛性質，即可確定下一次疊代時的尺度矩陣A²。

基本介紹

• 中文名：尺度矩陣
• 外文名：metric matrix
• 所屬學科：數學
• 簡介：擬牛頓法修正公式中的矩陣

基本介紹

第k+1次疊代尺度矩陣即

式中

詳細介紹

通過放大或縮小變數的各個坐標，也就是通過變數的尺度變換可以把函式的偏心程度降到最低限度。通過尺度變換能顯著改善幾乎所有極小化方法的收斂性質。

對於二次函式

若進行尺度變換

那么在新的坐標系中，函式的二次項將變為

選擇這樣變換的目的，是為了降低二次項的偏心程度。若矩陣G是正定的，則總存在矩陣Q使

(其中為單位矩陣)將函式偏心度變為零。

用Q^-1右乘等式兩邊，得

再用Q左乘等式兩邊，得

所以

這說明二次函式矩陣G的逆陣，可以通過尺度變換矩陣Q來求得。

牛頓法疊代公式為

梯度法疊代公式為

通過對牛頓法疊代公式和梯度法疊代公式的比較可以看出，二者的不同之處就在於牛頓法疊代公式中多了QQ^T部分。QQ^T實際上是在X空間內測量距離大小的一種度量，稱作尺度矩陣，記作H，即

在進行尺度變換前，向量X長度的概念是

尺度變換後向量X對於H尺度下的長度是

在這樣的長度定義下，確定“長度”這個純量大小時，使得某些方向起的作用比較大，而另一些方向起的作用比較小。為了使這種尺度有用，必須對一切非零向量X均要求，即要求尺度矩陣H正定。既然牛頓法疊代公式可用尺度變換矩陣表示出來，即

它和梯度法疊代公式只差一個尺度矩陣H，那么牛頓法就可看成是經過尺度變換後的梯度法。

經過尺度變換後，函式偏心率減小到零，函式的等值面變為球面(或超球面)，使設計空間中任意點處函式的梯度都通過極小點，用最速下降法只需一次疊代就可達到極小點。對變換前的二次函式，在使用牛頓方法時，由於其牛頓方向直接指向極小點，因此只需一次疊代就能找到極小點。