基本介紹
相關歷史
標準型
同型類別
正交拉丁方陣
定義

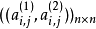

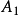

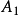

構造

特點
正交拉丁方
定理

套用
判斷拉丁方陣
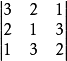


拉丁方一般指本詞條






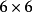
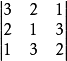

拉丁方設計(Latin square design)是以表格的形式被概念化,其中行和列代表兩個外部變數中的區組,然後將自變數的級別分配到表中各單元中。簡單的說就是某一變數在...
希臘拉丁方亦稱“正交拉丁方”,試驗設計的一種。由兩個互相正交的拉丁方重疊而成。本質上可以與正交表互變。三階希臘拉丁方可用於四因子,每個因子各有三個水平的...
拉丁方問題(problems of Latin square)組合數學的著名難題之一一個n階方陣,它的每一行及每一列都是n元有限集S的所有元素的一個排列,稱此方陣為集合S上的n階...
拉丁方陣(英語:Latin square)是一種 n × n 的方陣,在這種 n × n 的方陣里,恰有 n 種不同的元素,每一種不同的元素在同一行或同一列里只出現一次。...
拉丁方試驗設計,是指在統計上能控制兩個不相互作用的外部變數,每個外部變數或分區變數被劃分為一個相等數目的級別且自變數也同樣被分為相同數目的級別,即拉丁方排列...
超希臘-拉丁方,即拉丁方陣(英語:Latin square),是一種 n × n 的方陣,在這種 n × n 的方陣里,恰有 n 種不同的元素,每一種不同的元素在同一行或同一...
拉丁方格(Latin square)是實驗中用來抵消誤差的一種平衡設計——拉丁方設計概念化而來的表格。...
兩個n階拉丁方在同一位置上的數依次配置成對時,如果這兩個有序數對恰好各不相同(一般處理方法為把當中某些行或列對調)(這種相同即經過有限次旋轉和鏡像對稱後...
行完備拉丁方(row complete Latin square)是一類特殊的拉丁方,若n元集X的任意相異元的有序偶在X上的某個n階拉丁方的行中作為相鄰元素的有序偶至少出現一次,...
在拉丁方設計中,三個因素要求相同的水平數,即行,列,字母數均相同,但在具體實踐中可能其中一個因素水平數較少,這時就不能採用完整的拉丁方設計,則可用不完全拉丁...
正交拉丁方設計是使用正交拉丁方安排的一種試驗方案,當存在m個相互正交的n階拉丁方時,用拉丁方的行和列分別表示兩個因素的n個水平,用這m個拉丁方的記號分別表示...
自正交拉丁方(self-orthogonal Latin square)是一類特殊的拉丁方,指與自身的轉置相正交的拉丁方,亦即(2,1,3)共軛正交拉丁方。v階自正交拉丁方存在的充分必要條件...
拉丁矩(Latin rectangle)是拉丁方的推廣。設X為n元集,A為X上的r×s陣列,若同行和同列都沒有重複的元素,則稱A為X上的一個r×s拉丁矩。特別地,當r=s=n...
正交對稱拉丁方是一類組合對象,與羅姆方等價。值得注意的是正交對稱拉丁方不同於通常的正交拉丁方。若t個n階冪等對稱拉丁方中每兩個構成正交對稱拉丁方,則稱它們...
正交拉丁方完備組(complete set of MOLS)一組特殊的正交拉丁方.指v-1個相互正交的v階拉T方.若X=UF
正交對角拉丁方(orthogonal diagonal Latin squares)是一類特殊的正交拉丁方,若一個v階拉丁方的主對角線(位置(i,i),1≤i≤v)與反對角線(位置(i,v+1-i),1...
尤登方(Youden square)亦稱尤登設計。如果從一個拉丁方中划去至少一列(或行)並將行(或列)因子看作區組因子,仍然成為一個平衡不完全區設計的話,則稱這個不...
8.2.3正交拉丁方套用舉例 1458.3平衡不完全區組設計 1478.3.1基本概念 1478.3.2關聯矩陣及其性質 1488.3.3三連繫 1528.4幾何設計 154...
第5章拉丁方試驗設計 5.1拉丁方簡介 5.2拉丁方設計的原理 5.3拉丁方設計的試驗布置 5.3.1單拉丁方設計的試驗布置 5.3.2多拉丁方設計的試驗布置 ...
研究方向為組合數學,主要從事組合設計及其在密碼上套用的研究工作,以區組設計、正交拉丁方、圖分解、擬群以及信息認證和密鑰管理的組合結構為主要研究對象. 所研究的...
,Q中元素個數稱為擬群的階,在n階擬群(Q,°)的乘法表中,第a行第b列的元素為a°b,若記L=(mab),mab=a°b,則由乘法表所得的陣列L是一個n階拉丁方。...
