自正交拉丁方(self-orthogonal Latin square)是一類特殊的拉丁方,指與自身的轉置相正交的拉丁方,亦即(2,1,3)共軛正交拉丁方。v階自正交拉丁方存在的充分必要條件是v≠2,3,6。
基本介紹
- 中文名:自正交拉丁方
- 外文名:self-orthogonal Latin square
- 所屬學科:數學
- 所屬領域:組合學(組合設計)
- 屬性:一類特殊的拉丁方
- 定義:與自身的轉置相正交的拉丁方
基本介紹
共軛正交拉丁方
相關性質定理
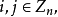
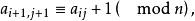
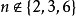

自正交拉丁方(self-orthogonal Latin square)是一類特殊的拉丁方,指與自身的轉置相正交的拉丁方,亦即(2,1,3)共軛正交拉丁方。v階自正交拉丁方存在的充分必要條件是v≠2,3,6。
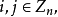
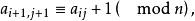
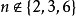
自正交拉丁方(self-orthogonal Latin square)是一類特殊的拉丁方,指與自身的轉置相正交的拉丁方,亦即(2,1,3)共軛正交拉丁方。v階自正交拉丁方存在的充分必要條件...
正交拉丁方編輯 鎖定 討論999 本詞條由“科普中國”科學百科詞條編寫與套用工作項目 審核。兩個n階拉丁方在同一位置上的數依次配置成對時,如果這兩個有序數對...
正交拉丁方設計是使用正交拉丁方安排的一種試驗方案,當存在m個相互正交的n階拉丁方時,用拉丁方的行和列分別表示兩個因素的n個水平,用這m個拉丁方的記號分別表示...
即為一對正交拉丁方。 而在階數固定的情況下,所有兩兩正交的拉丁方所成的集合稱為正交拉丁方族。拉丁方陣構造 請你造一個n=4的正交拉丁方陣。如果...
正交拉丁方完備組(complete set of MOLS)一組特殊的正交拉丁方.指v-1個相互正交的v階拉T方.若X=UF
超希臘-拉丁方,即拉丁方陣(英語:Latin square),是一種 n × n 的方陣,在這種 n × n 的方陣里,恰有 n 種不同的元素,每一種不同的元素在同一行或同一...
先後主持過河南省科委項目“框架結構的自正交拉丁方的存在性”等。合作主編了由中國科學技術出版社出版的《統計學》一書。1996年以第一完成者獲河南省自然科學優秀...
研究方向為組合數學,主要從事組合設計及其在密碼上套用的研究工作,以區組設計、正交拉丁方、圖分解、擬群以及信息認證和密鑰管理的組合結構為主要研究對象. 所研究的...
可分解配偶迴避混合雙打循環賽(resolvablespouse-avoiding mixed doubles round-robin)一種特定的循環賽.相應於一種自正交拉丁方.在配偶迴避的混合雙打循環賽(參見“...
